题目内容
【题目】某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：
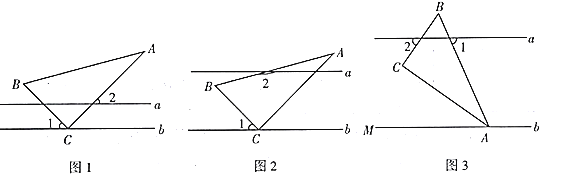
如图1，已知：在
中，
，
，直线m经过点A，
直线m，
直线m，垂足分别为点D、
试猜想DE、BD、CE有怎样的数量关系，请直接写出；
组员小颖想，如果三个角不是直角，那结论是否会成立呢？如图2，将中的条件改为：在中，，D、A、E三点都在直线m上，并且有
其中
为任意锐角或钝角
如果成立，请你给出证明；若不成立，请说明理由．
数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：
如图3，F是
角平分线上的一点，且
和
均为等边三角形，D、E分别是直线m上A点左右两侧的动点
、E、A互不重合
，在运动过程中线段DE的长度始终为n，连接BD、CE，若
，试判断
的形状，并说明理由．
【答案】
，理由见解析；
结论
成立；理由见解析；
为等边三角形，理由见解析.
【解析】
（1）先利用同角的余角相等，判断出
，进而判断△ADB≌△CEA，得出BD=AE，AD=CE，即可得出结论；
（2）先利用三角形内角和及平角的性质，判断出，进而判断出△ADB≌△CEA，得出BD=AE，AD=CE，即可得出结论；
（3）由（2）得，△ADB≌△CEA，得出BD=AE，再判断出△FBD≌△FAE，得出
，进而得出
，即可得出结论．
，
理由：
，
，
，
，
，
，
，
在
和
中，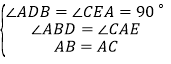
，
≌
，
，
，
，
故答案为：；
解：结论成立；
理由如下：
，
，
，
，
在
和
中，
，
≌
，
，，
；
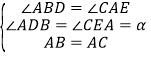为等边三角形，
理由：由得，≌，
，，
，即
，
在
和
中，
，
≌
，
，
，
，
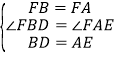为等边三角形．
故答案为：（1）DE=BD+CE，理由见解析；（2）结论DE=BD+CE成立；理由见解析；（3）△DFE为等边三角形，理由见解析.
练习册系列答案
相关题目
