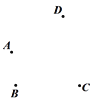题目内容
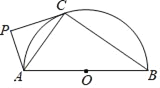
【题目】(1)问题背景:已知:如图①-1,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() ,试探究
,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)
之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)

解:(1)![]() 与
与![]() 、
、![]() 之间的数量关系是:
之间的数量关系是:![]() (或
(或![]() 只要关系式形式正确即可)
只要关系式形式正确即可)
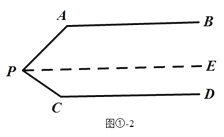
理由:如图①-2,过点![]() 作
作![]() .
.
∵![]() (作图),
(作图),
∴![]() ( ),
( ),
∴![]() (已知)
(已知)
![]() (作图),
(作图),
∴![]() _______( ),
_______( ),
∴![]() _______( ),
_______( ),
∴![]() (等量代换)
(等量代换)
又∵![]() (角的和差),
(角的和差),
∴![]() (等量代换)
(等量代换)
总结反思:本题通过添加适当的辅助线,从而利用平行线的性质,使问题得以解决.
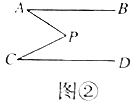
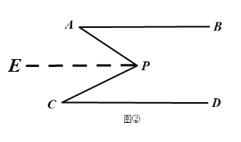
(2)类比探究:如图②,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() 、
、![]() ,请同学们类比(1)的解答过程,试探究
,请同学们类比(1)的解答过程,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.
之间有什么数量关系,并说明理由.
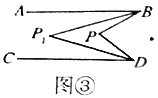
(3)拓展延伸:如图③,![]() ,
,![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数,请直接写出结果,不说明理由.
的度数,请直接写出结果,不说明理由.
【答案】(1)∠APC+∠PAB+∠PCD=360°,理由见解析;两直线平行,同旁内角互补;CD,如果两条直线都和第三条直线平行,那么这两条直线也互相平行;180°,两直线平行,同旁内角互补;(2)∠APC=∠PAB+∠PCD,理由见解析;(3)∠P=56°.
【解析】
(1)如图②,过点P作PE∥AB,依据平行线的性质,即可得到![]() 与
与![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(2)过点P作PE∥AB,依据平行线的性质,即可得出∠APE=∠PAB,∠CPE=∠PCD,进而得到∠APC=∠APE+∠CPE,即可得到∠APC=∠PAB+∠PCD;
(3)根据角平分线的性质及平行线的性质求解即可.
(1)∠APC与∠PAB、∠PCD之间的关系是:∠APC+∠PAB+∠PCD=360°
(或∠APC=360°-(∠PAB+∠PCD)只要关系式形式正确即可)
理由:如图①-2,过点P作PE∥AB.
∵PE∥AB(作图),
∴∠PAB+∠APE=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
PE∥AB(作图),
∴PE∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠CPE+∠PCD=180°(两直线平行,同旁内角互补),
∴∠PAB+∠APE+∠CPE+∠PCD=180°+180°=360°(等量代换)
又∵∠APE+∠CPE=∠APC(角的和差),
∴∠APC+∠PAB+∠PCD=360°(等量代换)
(2)∠APC与∠PAB、∠PCD之间的关系是:∠APC=∠PAB+∠PCD
理由:过点P作PE∥AB,
∴∠PAB=∠APE(两直线平行,内错角相等)
∵AB∥CD(已知)
PE∥AB(作图),
∴PE∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠PCD=∠CPE(两直线平行,内错角相等)
∵∠APE+∠CPE=∠APC(角的和差),
∴∠APC=∠PAB+∠PCD(等量代换)
(3)∠P=56°.

理由:如图③,∵![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,
∴∠PBA=2∠![]() BA, ∠PDC=2∠
BA, ∠PDC=2∠![]() DC,
DC,
∴∠PBA+ ∠PDC=2(∠![]() BA+
BA+![]() DC)
DC)
由(2)可得: ∠P=∠PBA+∠PDC, ∠![]() =∠AB
=∠AB![]() +∠CD
+∠CD![]()
∴∠P=2(∠![]() BA+
BA+![]() DC)=2∠
DC)=2∠![]() =2×28°=56°
=2×28°=56°

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案