题目内容
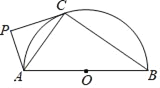
【题目】如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
求证:(1)∠PAC=∠CAB;
(2)AC2=APAB.
【答案】见解析
【解析】
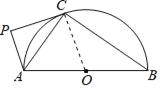
(1)如下图,连接OC,由已知易得OC⊥PC,结合AP⊥PC可得OC∥AP,从而可得∠PAC=∠ACO,结合∠ACO=∠CAO即可得到∠PAC=∠CAB;
(2)由已知易得∠APC=∠ACB=90°,结合(1)中所得∠PAC=∠CAB可得△PAC∽△CAB,
这样即可由相似三角形的性质证得:AC2=APAB.
(1)连结OC,如图.
∵直线PC切半圆O于点C,
∴OC⊥PC,
∵AP⊥PC,
∴OC∥AP,
∴∠PAC=∠OCA,
∵OC=OA,
∴∠CAB=∠OCA,
∴∠PAC=∠CAB;
(2)∵AB为半圆O的直径,
∴∠ACB=90°,
∵AP⊥PC,
∴∠P=∠ACB,
又∵由(1)可知∠PAC=∠CAB,
∴△PAC∽△CAB,
∴![]() ,
,
∴AC2=APAB.

练习册系列答案
相关题目