Question

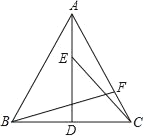
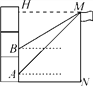
【题目】 如图，在四边形ABCD中，AD∥BC，AB⊥BC，对角线AC⊥CD，点E在边BC上，且∠AEB=45°，CD=10．

（1）求AB的长；

（2）求EC的长．

Answer 1

【答案】（1）5；（2）155.

【解析】

（1）在Rt△ACD中，根据勾股定理可求AC=10，∠DAC=30°，根据平行线的性质得到∠ACB=30°，在Rt△ACB中，根据含30度角的直角三角形可求AB的长；

（2）在Rt△ABE中，根据等腰直角三角形的性质可求BE，BC，再根据EC=BC-BE即可求解．

(1)在Rt△ACD中,∵∠D=60°，CD=10，

∴AD=20，

∴AC= =10,∠DAC=30°，

又∵AD∥BC，

∵∠ACB=∠DAC=30°，

∴在Rt△ACB中，

AB=AC==5.

(2)在Rt△ABE中,∠AEB=45°，

∴BE=AB=5，

由(1)可知,BC==15，

∴EC=BCBE=155.