题目内容
【题目】函数y=ax2+bx+c (a,b,c为常数,且a≠0)经过点(﹣1,0)、(m,0),且1<m<2,当x<﹣1时,y随x增大而减小,下列结论:①abc>0;②a+b<0;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0;⑤c≤﹣1时,则b2﹣4ac≤4a.其中结论正确的有( )个
A. 5 B. 4 C. 3 D. 2
【答案】D
【解析】根据题意画出抛物线的大致图象,利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,于是可对①进行判断;由于抛物线过点(-1,0)和(m,0),且1<m<2,根据抛物线的对称性和对称轴方程得到0<![]() <
<![]() ,变形可得a+b>0,则可对②进行判断;利用点A(-3,
,变形可得a+b>0,则可对②进行判断;利用点A(-3,![]() )和点B(3,
)和点B(3,![]() )到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a-b+c=0,
)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a-b+c=0,![]() ,两式相减得
,两式相减得![]() ,然后把等式左边分解后即可得到a(m-1)+b=0,则可对④进行判断;根据顶点的纵坐标公式和抛物线对称轴的位置得到
,然后把等式左边分解后即可得到a(m-1)+b=0,则可对④进行判断;根据顶点的纵坐标公式和抛物线对称轴的位置得到![]() ,变形得到
,变形得到![]() ,则可对⑤进行判断
,则可对⑤进行判断
如图,
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,
所以①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴0<﹣![]() <
<![]() ,
,
∴![]() +
+![]() =
=![]() >0,
>0,
∴a+b>0,
所以②的结论错误;
∵点A(﹣3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,
∴y1>y2,
所以③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,
所以④的结论正确;
∵![]() <c,
<c,
而c≤﹣1,
∴![]() <﹣1,
<﹣1,
∴b2﹣4ac>4a,所以⑤的结论错误.
故选:D.

【题目】为了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计表.调查结果统计表
组别 | 分组(单位:元) | 人数 |
|
| 4 |
|
| 16 |
|
|
|
|
|
|
|
| 2 |
调查结果扇形统计图
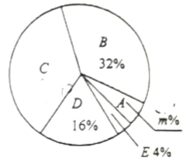
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有 人, ,
![]()
![]() ;
;
(2)求扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(3)若该校共有学生1000人,请估计每月零花钱的数额![]() 在
在![]() 范围的人数.
范围的人数.