题目内容
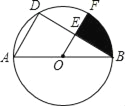
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
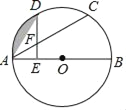
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
【答案】(1)①②详见解析;③3![]() ﹣4;(2)13.
﹣4;(2)13.
【解析】
(1)①由旋转性质知AB=AD,∠BAD=60°即可得证;②由BA=BD、EA=ED根据中垂线性质即可得证;③分别求出BF、EF的长即可得;
(2)由∠ACB+∠BAC+∠ABC=180°、∠DAG+∠DAE+∠BAE=180°、∠DAG=∠ACB、∠DAE=∠BAC得∠BAE=∠BAC且AE=AC,根据三线合一可得CE⊥AB、AC=5、AH=3,继而知CE=2CH=8、BE=5,即可得答案.
(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=BD,
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC,
∴EA=ED,
∴点B、E在AD的中垂线上,
∴BE是AD的中垂线,
∵点F在BE的延长线上,
∴BF⊥AD, AF=DF;
③由②知BF⊥AD,AF=DF,
∴AF=DF=3,
∵AE=AC=5,
∴EF=4,
∵在等边三角形ABD中,BF=ABsin∠BAF=6×![]() =3
=3![]() ,
,
∴BE=BF﹣EF=3![]() ﹣4;
﹣4;
(2)如图所示,
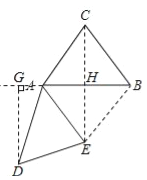
∵∠DAG=∠ACB,∠DAE=∠BAC,
∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°,
又∵∠DAG+∠DAE+∠BAE=180°,
∴∠BAE=∠ABC,
∵AC=BC=AE,
∴∠BAC=∠ABC,
∴∠BAE=∠BAC,
∴AB⊥CE,且CH=HE=![]() CE,
CE,
∵AC=BC,
∴AH=BH=![]() AB=3,
AB=3,
则CE=2CH=8,BE=5,
∴BE+CE=13.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案