题目内容
【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).
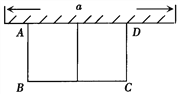
(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
【答案】(1)AB长为5米(2)最大面积为![]()
【解析】试题分析:
(1)由题意可知围成该花圃需要用到篱笆的宽有三条,而长只有一条,设宽AB的长为xm,则长BC为(24-3x)m,再设长方形面积为y,由矩形面积公式可得:y关于x的函数关系式,由y=45解得对应的x的值,可得答案;
(2)把(1)中所得解析式配方化为顶点式,然后结合自变量的取值范围可求得y的最大值,把最大值与45比较可得结论,并进一步可由自变量的取值范围和解析式求得最大面积;
试题解析:
(1)设花圃的宽AB=x米,知BC应为(24-3x)米,故面积y与x的关系式为
y=x(24-3x)=-3x2+24x.
当y=45时,-3x2+24x=45,解出x1=3,x2=5.
当x2=3时,BC=24-3×3>10,不合题意,舍去;
当x2=5时,BC=24-3×5=9,符合题意.
故AB长为5米.
(2)能围成面积比45m2更大的矩形花圃.
由(1)知,y=-3x2+24x=-3(x-4)2+48,
∵![]() ,∴
,∴![]() ,
,
由抛物线y=-3(x-4)2+48知,在对称轴x=4的右侧,y随x的增大而减小,
∴当![]() 时,y=-3(x-4)2+48有最大值,且最大值为
时,y=-3(x-4)2+48有最大值,且最大值为![]() 此时,
此时, ![]() BC=10m,即围成长为10米,宽为
BC=10m,即围成长为10米,宽为![]() 米的矩形ABCD花圃时,其最大面积为
米的矩形ABCD花圃时,其最大面积为![]()

【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.