Question

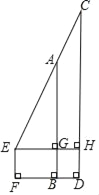
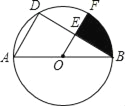
【题目】如图所示，AB是⊙O的直径，AB=4，D是⊙O上的一点，∠ABD=30°，OF∥AD交BD于点E，交⊙O于点F．

（1）求DE的长度；

（2）求阴影部分的面积（结果保留π）．

Answer 1

【答案】（1）；（2）π﹣；

【解析】

（1）利用圆周角定理、余弦三角函数的定义求得BD=2；然后由三角形中位线的定义证得点E是线段BD的中点，即DE=BD求得；
（2）阴影部分的面积=扇形OFB的面积-△OBE的面积．

（1）∵AB是⊙O的直径，

∴∠ADB=90°（直径所对的圆周角是直角）；

又∠ABD=30°，AB=4，

∴BD=ABcos∠ABD=4×=2；

∵OF∥AD，点O是AB的中点，

∴OE是△ABD的中位线，

∴点E是线段BD的中点，

∴DE=BD=；

（2）由（1）知，∠ADB=90°．

∵∠ABD=30°，

∴∠DAB=60°（三角形内角和定理）；

又∵OF∥AD，

∴∠EOB=∠DAB=60°（两直线平行，同位角相等）；

∵OB=AB=2，

∴S扇形OBF=；

由（1）知，DE=BD，

∴BE=BD=，

∴S△OBE=OBBEsin∠EBO=×2××=，

∴S阴影=S扇形OBF﹣S△OBE=π﹣．