题目内容
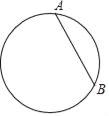
【题目】如图,已知圆上两点A,B.
(1)用直尺和圆规求作圆心(保留作图痕迹,不写画法);
(2)若AB=6,此圆的半径为2![]() ,求弦AB与劣弧AB所组成的弓形面积.
,求弦AB与劣弧AB所组成的弓形面积.
【答案】(1)见解析;(2)4π﹣3![]() ;
;
【解析】
(1)任意作出不同于AB的弦,然后作出弦AB、AC的垂直平分线,相交于点O,则点O即为所求;
(2)由OD⊥AB,勾股定理计算出OD,这样可得到∠AOB=120°,而S弓形AB=S扇形OAB-S△AOB,然后利用扇形和三角形的面积公式计算即可.
(1)如图所示,点O即为所求;
(2)如图,连接OA,OB,
∵OC⊥AB,
∴AC=BC,
而弦AB=6,
∴AD=3,
又∵⊙O的半径长为2![]() ,
,
∴OD=![]() ,
,
∴∠OAB=30°,
∴∠AOB=120°,
∴S弓形AB=S扇形OAB﹣S△AOB=![]() ×
×![]() ×6=4π﹣3
×6=4π﹣3![]() .
.
所以弓形AB的面积4π﹣3![]() .
.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目