Question

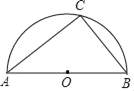
【题目】如图，在半径为的扇形中，，点是弧上的一个动点（不与点、重合），，垂足分别为、．

当时，求线段的长；

在中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；

设，的面积为，求关于的函数关系式，并写出的范围．

Answer 1

【答案】(1) ;(2)见解析;(3)见解析.

【解析】

（1）图（1）中，根据垂径定理可得BD＝BC，然后只需运用勾股定理即可求出线段OD的长；

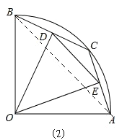
（2）连接AB，如图（2），用勾股定理可求出AB的长，根据垂径定理可得D和E分别是线段BC和AC的中点，根据三角形中位线定理就可得到DE=AB，DE保持不变；

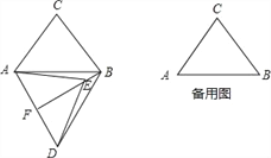
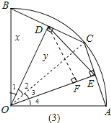
（3）过D作DF⊥OE于F，连接OC，如图（3），运用等腰三角形的性质可推出∠DOE=45°，在Rt△OFD中，运用三角函数可求出OF、DF，在Rt△DFE中，运用勾股定理可求出EF，从而求出OE，就可解决问题．

)如图，

∵，

∴．

∵，，，

∴，

即线段的长为；

存在，保持不变．

理由：连接，如图，

∵，，

∴，

∵，，

∴和分别是线段和的中点，

∴，

∴保持不变；

过作于，连接，如图．

∵，，，

∴，

∵，，，

∴，，

∴，即，

在中，

∵，，

∴，

，

在中，

∵，，

∴，

∴，

∴．