Question

【题目】小明在学习过程中，对教材中的一个有趣问题做如下探究：

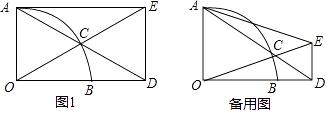
（习题回顾）已知：如图1，在中，，是角平分线，是高，、相交于点.求证：；

（变式思考）如图2，在中，，是边上的高，若的外角的平分线交的延长线于点，其反向延长线与边的延长线交于点，则与还相等吗？说明理由；

（探究延伸）如图3，在中，上存在一点，使得，的平分线交于点.的外角的平分线所在直线与的延长线交于点.直接写出与的数量关系.

Answer 1

【答案】[习题回顾]证明见解析；[变式思考] 相等，证明见解析；[探究延伸] ∠M+∠CFE=90°，证明见解析．

【解析】

[习题回顾]根据同角的余角相等可证明∠B=∠ACD，再根据三角形的外角的性质即可证明；

[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF、再根据直角三角形的性质和等角的余角相等即可得出=；

[探究延伸]根据角平分线的定义可得∠EAN=90°，根据直角三角形两锐角互余可得∠M+∠CEF=90°，再根据三角形外角的性质可得∠CEF=∠CFE，由此可证∠M+∠CFE=90°．

[习题回顾]证明：∵∠ACB=90°，CD是高，
∴∠B+∠CAB=90°，∠ACD+∠CAB=90°，
∴∠B=∠ACD，
∵AE是角平分线，
∴∠CAF=∠DAF，
∵∠CFE=∠CAF+∠ACD，∠CEF=∠DAF+∠B，
∴∠CEF=∠CFE；

[变式思考]相等，理由如下：
证明：∵AF为∠BAG的角平分线，
∴∠GAF=∠DAF，

∵∠CAE=∠GAF，

∴∠CAE=∠DAF，
∵CD为AB边上的高，∠ACB=90°,
∴∠ADC=90°，
∴∠ADF=∠ACE=90°，

∴∠DAF+∠F=90°，∠E+∠CAE=90°，
∴∠CEF=∠CFE；

[探究延伸]∠M+∠CFE=90°，
证明：∵C、A、G三点共线AE、AN为角平分线，
∴∠EAN=90°，

又∵∠GAN=∠CAM，
∴∠M+∠CEF=90°，
∵∠CEF=∠EAB+∠B，∠CFE=∠EAC+∠ACD，∠ACD=∠B，
∴∠CEF=∠CFE，
∴∠M+∠CFE=90°．