题目内容
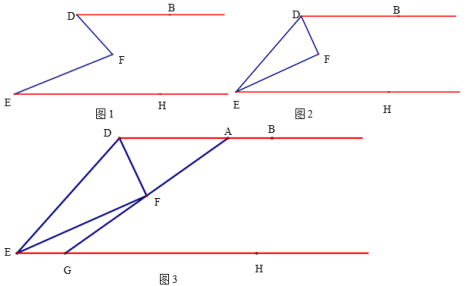
【题目】已知DB∥EH,F是两条射线内一点,连接DF、EF.
(1)如图1:求证:∠F=∠D+∠E;
(2)如图2:连接DE,∠BDE、∠HED的角平分交于点F时,求∠F的度数;
(3)在(2)条件下,点A是射线DB上任意一点,连接AF,并延长交EH于点G,求证:AF=FG.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)过点F作FM∥BD,则FM∥HE,又根据FM∥BD,即可有∠1=∠D,∠2=∠E,则可证明∠F=∠D+∠E;(2)根据角平分线得出∠3=∠5,∠4=∠6,DB∥HE得出∠3+∠5+∠4+∠6=1800,即可证明∠F=900;(3)过F点作BD的垂线,垂足为K,延长KF交EH于点I;过F点作FJ垂线于点J,根据DA∥EH得出∠AKF=∠GIF=900,由角平分线得出KF=FJ,FI=FJ,所以KF=FI,则可证明△AKF≌△GIF,所以AF=FG.
(1)过点F作FM∥BD,则FM∥HE,

∵FM∥BD,FM∥HE
∴∠1=∠D,∠2=∠E
∵∠F=∠1+∠2
∴∠F=∠D+∠E
(2)
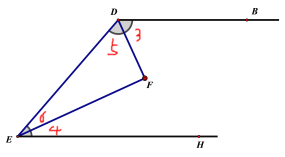
∵DF是角平分线
∴∠3=∠5
又∵EF是角平分线
∴∠4=∠6
又∵DB∥HE
∴∠3+∠5+∠4+∠6=1800
∴∠5+∠6=900
∴∠F=900
(3)过F点作BD的垂线,垂足为K,延长KF交EH于点I;过F点作FJ垂线于点J

∵DA∥EH
∴∠AKF=∠GIF=900
∵DF是角平分线
∴KF=FJ
EF是角平分线
∴FI=FJ
∴KF=FI
在△AKF和△GIF中

∴△AKF≌△GIF(AAS)
∴AF=FG

练习册系列答案
相关题目