题目内容
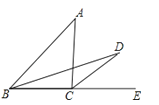
【题目】如图，AB∥CD，OA=OD，点F、D、O、A、E在同一直线上，AE=DF，求证：EB∥CF．
【答案】证明见解析
【解析】试题分析：由AB与CD平行，利用两直线平行得到两对内错角相等，再由OA=OD，利用AAS得到△AOB≌△DOC，利用全等三角形对应边相等得到OC=OB，由OA+AE=OD+DF求出OF=OE，夹角为对顶角相等，利用SAS得到△COF≌△BOE，利用全等三角形对应角相等得到一对内错角相等，利用内错角相等两直线平行即可得证．
试题解析：∵AB∥CD， ∴∠DCO=∠ABO，∠CDO=∠BAO， 在△AOB和△DOC中，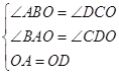
， ∴△AOB≌△DOC（AAS）， ∴OC=OB， ∵OA=OD，AE=DF， ∴OA+AE=OD+DF，即OE=OF， 在△COF和△BOE中，
， ∴△COF≌△BOE（SAS）， ∴∠F=∠E， ∴BE∥CF．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
