题目内容
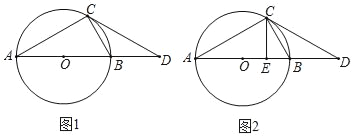
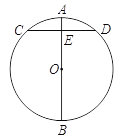
【题目】如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为_______.
【答案】![]()
【解析】
连接OD,AD,根据已知可得OC平分∠BCD,根据BC=DC,即可得到BD⊥CO,根据已知可以推得CO⊥BD,再根据AB为直径,继而可得AD//CO,结合AE=AO=2,则可得AD=1,在Rt△ABD中,利用勾股定理即可求得BD的长.
连接OD,AD,
∵BC=CD,BO=DO,
∴∠1=∠2,∠3=∠DBO,
∴∠1+∠3=∠2+∠DBO,∴∠CDO=∠CBO,
∵OC=OB=OD,
∴∠BCO=∠DCO,
∴CO为等腰△BCD的角平分线,
∴CO⊥BD,
∵AB为直径,
∴∠ADB=90°,
∴∠3+∠5=∠3+∠4=90°,
∴∠4=∠5,
∴AD//CO,
∵AE=AO=2,∴AD=![]() CO=1,
CO=1,
在Rt△ABD中,BD=![]() .
.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目