题目内容
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为45°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走4米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，那么大树CD的高度为_____．
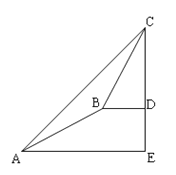
【答案】11
【解析】
可以作BF⊥AE于F，在Rt△ABF中，运用勾股定理，根据各边的数量关系求得AF的长度，就可得到AE的长度；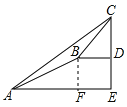
接下来根据已知的AE的长度，在Rt△ACE中，运用三角函数求得CE的长度，进而可知CD的长度.
解：作BF⊥AE于F，如图所示：
则FE=BD=4米，DE=BF.
∵斜面AB的坡度i=1:2.4，
∴AF=2.4BF.
设BF=x米，则AF=2.4x米，
在Rt△ABF中，由勾股定理得：x2+(2.4x)2=132，
解得：x=5，
∴DE=BF=5米，AF=12米，
∴AE=AF+FE=16米.
在Rt△ACE中，CE=AE=16米，
∴CD=CE-DE=16米-5米=11米.
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
（1）根据上表填空：
①抛物线与x轴的交点坐标是_________和_________；
②抛物线经过点（-3，_________）；
（2）试确定抛物线y=ax2+bx+c的解析式.
