ƒøƒ⁄»ð
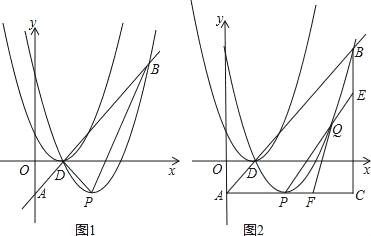
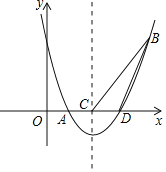
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝y=![]() x2+bx+cµƒÕºœÛΩªx÷·”⁄A£¨D¡Ωµ„£¨≤¢æ≠π˝Bµ„£¨∂‘≥∆÷·Ωªx÷·”⁄µ„C£¨¡¨Ω”BD£¨BC£¨“—÷™Aµ„◊¯±Í «£®2£¨0£©£¨Bµ„µƒ◊¯±Í «£®8£¨6£©
x2+bx+cµƒÕºœÛΩªx÷·”⁄A£¨D¡Ωµ„£¨≤¢æ≠π˝Bµ„£¨∂‘≥∆÷·Ωªx÷·”⁄µ„C£¨¡¨Ω”BD£¨BC£¨“—÷™Aµ„◊¯±Í «£®2£¨0£©£¨Bµ„µƒ◊¯±Í «£®8£¨6£©
£®1£©«Û∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£Æ
£®2£©«Û∏√∫Ø ˝ÕºœÛµƒ∂•µ„◊¯±Íº∞Dµ„µƒ◊¯±Í£Æ
£®3£©≈◊ŒÔœþ…œ”–“ª∏ˆ∂ص„P£¨”ÎA£¨D¡Ωµ„ππ≥…°˜ADP£¨ «∑ҥʑ⁄S°˜ADP=![]() S°˜BCD£ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–∑˚∫œÃıº˛µƒµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£Æ«ÎÀµ√˜¿Ì”…£Æ
S°˜BCD£ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–∑˚∫œÃıº˛µƒµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£Æ«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø(1) y=![]() x2-4x+6£ª (2) ≈◊ŒÔœþµƒ∂•µ„◊¯±ÍŒ™£®4£¨6£©£¨D£®6£¨0£©£ª(3)¥Ê‘⁄£¨Pµ„◊¯±ÍŒ™£®4+
x2-4x+6£ª (2) ≈◊ŒÔœþµƒ∂•µ„◊¯±ÍŒ™£®4£¨6£©£¨D£®6£¨0£©£ª(3)¥Ê‘⁄£¨Pµ„◊¯±ÍŒ™£®4+![]() £¨
£¨![]() £©ªÚ£®4-
£©ªÚ£®4-![]() £¨
£¨![]() £©ªÚ£®3£¨-
£©ªÚ£®3£¨-![]() £©ªÚ£®5£¨-
£©ªÚ£®5£¨-![]() £©£Æ
£©£Æ
°æΩ‚Œˆ°ø
£®1£©¿˚”√¥˝∂®œµ ˝∑®«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©∞—£®1£©÷–µƒΩ‚Œˆ Ω≈‰≥…∂•µ„ Ωø…µ√µΩ∂•µ„◊¯±Í£¨»ª∫Û¿˚”√≈◊ŒÔœþµƒ∂‘≥∆–‘»∑∂®Dµ„◊¯±Í£ª
£®3£©…ËP£®x£¨![]() x2-4x+6£©£¨¿˚”√»˝Ω«–Œ√ʪ˝π´ Ωµ√µΩ
x2-4x+6£©£¨¿˚”√»˝Ω«–Œ√ʪ˝π´ Ωµ√µΩ![]() £®6-2£©|
£®6-2£©|![]() x2-4x+6|=
x2-4x+6|=![]() °¡
°¡![]() °¡£®6-4£©°¡6£¨‘Úx2-8x+9=0ªÚx2-8x+15=0£¨»ª∫Û∑÷±Ω‚¡Ω∏ˆ“ª‘™∂˛¥Œ∑Ω≥ú¥ø…µ√µΩPµ„◊¯±Í£Æ
°¡£®6-4£©°¡6£¨‘Úx2-8x+9=0ªÚx2-8x+15=0£¨»ª∫Û∑÷±Ω‚¡Ω∏ˆ“ª‘™∂˛¥Œ∑Ω≥ú¥ø…µ√µΩPµ„◊¯±Í£Æ
£®1£©∞—A£®2£¨0£©£¨B£®8£¨6£©¥˙»Îy=![]() x2+bx+cµ√
x2+bx+cµ√
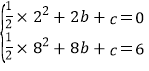 £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=![]() x2-4x+6£ª
x2-4x+6£ª
£®2£©°þy=![]() x2-4x+6=
x2-4x+6=![]() £®x-4£©2+6£¨
£®x-4£©2+6£¨
°ý≈◊ŒÔœþµƒ∂•µ„◊¯±ÍŒ™£®4£¨6£©£¨
°þ≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™÷±œþx=4£¨A£®2£¨0£©£¨
°ýD£®6£¨0£©£ª
£®3£©¥Ê‘⁄£Æ
…ËP£®x£¨![]() x2-4x+6£©£¨
x2-4x+6£©£¨
°þS°˜ADP=![]() S°˜BCD£¨
S°˜BCD£¨
°ý![]() £®6-2£©|
£®6-2£©|![]() x2-4x+6|=
x2-4x+6|=![]() °¡
°¡![]() °¡£®6-4£©°¡6£¨
°¡£®6-4£©°¡6£¨
°ýx2-8x+9=0ªÚx2-8x+15=0£¨
Ω‚∑Ω≥Ãx2-8x+9=0µ√x1=4+![]() £¨x2=4-
£¨x2=4-![]() £¨¥À ±Pµ„◊¯±ÍŒ™£®4+
£¨¥À ±Pµ„◊¯±ÍŒ™£®4+![]() £¨
£¨![]() £©ªÚ£®4-
£©ªÚ£®4-![]() £¨
£¨![]() £©£ª
£©£ª
Ω‚∑Ω≥Ãx2-8x+15=0µ√x1=3£¨x2=5£¨¥À ±Pµ„◊¯±ÍŒ™£®3£¨-![]() £©ªÚ£®5£¨-
£©ªÚ£®5£¨-![]() £©£ª
£©£ª
◊€…œÀ˘ ˆ£¨Pµ„◊¯±ÍŒ™£®4+![]() £¨
£¨![]() £©ªÚ£®4-
£©ªÚ£®4-![]() £¨
£¨![]() £©ªÚ£®3£¨-
£©ªÚ£®3£¨-![]() £©ªÚ£®5£¨-
£©ªÚ£®5£¨-![]() £©£Æ
£©£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏