Question

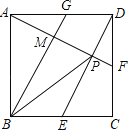
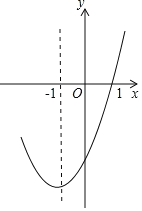
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1，图象过（1，0）点，部分图象如图所示，下列判断中：

①abc＞0；

②b2﹣4ac＞0；

③9a﹣3b+c=0；

④若点（﹣0.5，y1），（﹣2，y2）均在抛物线上，则y1＞y2；

⑤5a﹣2b+c＜0．

其中正确的个数有（　　）

A.2B.3C.4D.5

Answer 1

【答案】B

【解析】

①根据抛物线开口方向，对称轴位置，以及与y轴的交点位置，得出a，b，c的正负性，即可可判断①；

②根据抛物线与ｙ轴有两个交点可得b2﹣4ac＞0；

③由抛物线的对称性得抛物线与x轴在左侧的交点为(-3,0)，代入解析式即可得9a﹣3b+c=0；

④找到(﹣0.5，y1)关于对称轴的对称点，再根据抛物线的增减性判断函数值大小；

⑤利用b=2a，c=﹣3a，代入5a﹣2b+c即可判断．

∵抛物线对称轴x=﹣1，经过(1，0)，

∴﹣=﹣1，a+b+c=0，

∴b=2a，c=﹣3a．

∵a＞0，

∴b＞0，c＜0，

∴abc＜0，故①错误．

∵抛物线与x轴有两个交点，

∴b2﹣4ac＞0，故②正确．

∵抛物线与x轴交于(﹣3，0)，

∴9a﹣3b+c=0，故③正确．

点(﹣0.5，y1)，(﹣2，y2)均在抛物线上，(﹣0.5，y1)关于x=-1的对称点为(﹣1.5，y1)

∵，抛物线在时，y随x的增大而减小，

∴y1＜y2；故④错误．

∵5a﹣2b+c=5a﹣4a﹣3a=﹣2a＜0，故⑤正确．

故选：B．