题目内容
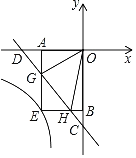
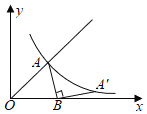
【题目】如图，如图，在菱形
中，
，
，把菱形绕点
顺时针旋转30°得到菱形
，其中点
的运动路径为
，则图中阴影部分的面积为_________．
【答案】π+6-4
【解析】
连接CD＇和BC＇，由菱形的性质以及旋转角为30°，可得A、D＇、C及A、B、C＇分别共线，求出扇形面积，再根据AAS证得两个小三角形全等，求得其面积，最后根据扇形ACC＇的面积-两个小的三角形面积即可解答．
解：CD＇和BC＇
∵在菱形
中，∠DAB=60°，
∴∠DAC=∠CAB=30°
∵旋转角为30°
∴A、D＇、C共线，同理：A、B、C＇共线；
∴AC=2
∴扇形ACC＇的面积为：
∵AC＝AC＇， AD＇=AB
∴在△OCD＇和△OC＇B中
∴△OCD＇≌△OC＇B（AAS）
∴OB＝OD＇， CO=OC＇
∵∠CBC＇=60°，∠BC＇O=30°
∴∠COD＇=90°
∴C D＇=AC＇-AD=2-2, OD＇=2- OC
∵AC=2
∴在Rt△D＇OC中，解得:OD＇=sin30°·C D＇=-1，OC= cos30°·C D＇=3-
∴S△D＇OC= S△OC＇B=2-3
∴阴影部分的面积为:π-2(2-3)= π+6-4
故答案为:π+6-4．
练习册系列答案
阅读快车系列答案
相关题目
