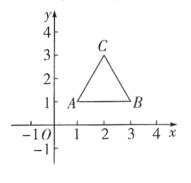题目内容
【题目】定义:如果一个直角三角形的两条直角边的比为![]() ,那么这个三角形叫做“半正切三角形”.
,那么这个三角形叫做“半正切三角形”.
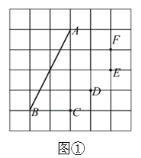

(1)如图①,正方形网格中,已知格点![]() ,
,![]() ,在格点
,在格点![]() ,
,![]() ,
,![]() ,
,![]() 中,与
中,与![]() ,
,![]() 能构成“半正切三角形”的是点__________;
能构成“半正切三角形”的是点__________;
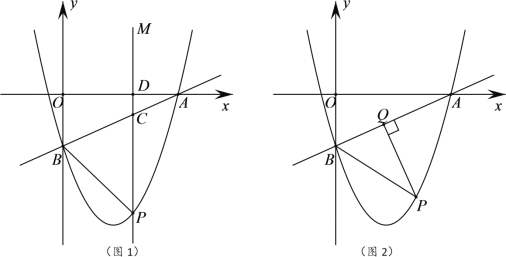
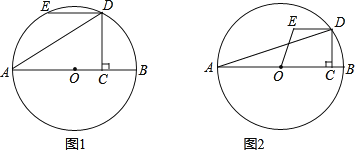
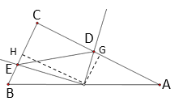
(2)如图②,![]() 为“半正切三角形”,点
为“半正切三角形”,点![]() 在斜边
在斜边![]() 上,点
上,点![]() 在边
在边![]() 上,将射线
上,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,所得射线交边
,所得射线交边![]() 于点
于点![]() ,连接
,连接![]() .
.
①小彤发现:若![]() 为斜边
为斜边![]() 的中点,则
的中点,则![]() 一定为“半正切三角形”.请判断“小彤发现”是否正确?并说明理由;
一定为“半正切三角形”.请判断“小彤发现”是否正确?并说明理由;
②连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)正确,见解析;(3)
;(2)正确,见解析;(3)![]()
【解析】
(1)按照“半正切三角形”的条件,逐个求解即可;
(2)①过![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,然后利用相似三角形的性质证明即可;
,然后利用相似三角形的性质证明即可;
②过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,也可证得
,也可证得![]() 也为“半正切三角形”,再利用相似三角形及三角函数计算即可.
也为“半正切三角形”,再利用相似三角形及三角函数计算即可.
解:(1)若为点C,在△ABC中,AB2=20,BC2=4,AC2=16,
则AB2=BC2+AC2,△ABC是直角三角形且AC=2BC,∴点C符合;
若为点D,在△ABD中,AB2=20,AD2=10,BD2=10,
则AB2=AD2+BD2,△ABD是直角三角形且AD=BD,∴点D不符合;
若为点E,在△ABE中,AB2=20,AE2=8,BE2=20,
则AB2≠AE2+BE2,△ABE不是直角三角形,∴点E不符合;
若为点F,在△ABF中,AB2=20,AF2=5,BF2=25,
则AB2+AF2=BF2,△ABF是直角三角形且BF=2AF,∴点F符合;
故答案为:![]() ,
,![]() .
.
(2)①过![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
则![]() .又
.又![]() ,∴
,∴![]() .
.
再证![]() .
.
又![]() ,
,
∴![]() 为“半正切三角形”.
为“半正切三角形”.
(3)解:由旋转可知![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,可得
,可得![]() 也为“半正切三角形”,
也为“半正切三角形”,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
则![]() .
.
∴![]() .
.

练习册系列答案
相关题目