题目内容
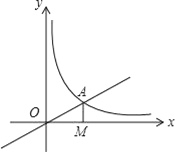
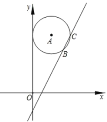
【题目】如图,在直角坐标系中,⊙A的圆心坐标为(![]() ,a)半径为
,a)半径为![]() ,函数y=2x﹣2的图象被⊙A截得的弦长为2,则a的值为_____.
,函数y=2x﹣2的图象被⊙A截得的弦长为2,则a的值为_____.
【答案】4![]() ﹣2
﹣2
【解析】
作AH⊥x轴于H,交CB于D,作AE⊥CB于E,连结AC,由题意得出![]()
![]() ,把
,把![]() 代入y=2x-2得
代入y=2x-2得![]() ,得出D点坐标为
,得出D点坐标为![]() ,得出HD=
,得出HD=![]() ,由垂径定理得出CE=BE=
,由垂径定理得出CE=BE=![]() ,由勾股定理得出
,由勾股定理得出![]() ,求出直线y=2x-2与坐标轴的交点坐标,得出OG=2,OF=1,由平行线的性质得出∠ADE=∠HDF=∠OGF,求出DE=2AE=4,由勾股定理得出
,求出直线y=2x-2与坐标轴的交点坐标,得出OG=2,OF=1,由平行线的性质得出∠ADE=∠HDF=∠OGF,求出DE=2AE=4,由勾股定理得出![]() ,即可得出结果.
,即可得出结果.
解:作AH⊥x轴于H,交CB于D,作AE⊥CB于E,连结AC,如图,

∵⊙A的圆心坐标为(![]() ,a),
,a),
∴OH=![]() ,AH=a,
,AH=a,
把x=![]() 代入y=2x﹣2得y=2
代入y=2x﹣2得y=2![]() ﹣2,
﹣2,
∴D点坐标为(![]() ,2
,2![]() ﹣2),
﹣2),
∴HD=2![]() ﹣2,
﹣2,
∵AE⊥CB,
∴CE=BE=![]() ,
,
在Rt△ACE中,AC=![]() ,
,
∴![]() ,
,
∵span>y=2x﹣2,
当x=0时,y=﹣2;当y=0时,x=1,
∴G(0,﹣2),F(1,0),
∴OG=2,OF=1,
∵AH∥y轴,
∴∠ADE=∠CDF=∠OGF,
∴tan∠ADE=![]() =tan∠OGF=
=tan∠OGF=![]() =
=![]() ,
,
∴DE=2AE=4,
∴AD=![]() =
=![]() =2
=2![]() ,
,
∴a=AH=AD+HD=2![]() +2
+2![]() ﹣2=4
﹣2=4![]() ﹣2,
﹣2,
故答案为:4![]() ﹣2.
﹣2.

练习册系列答案
相关题目