题目内容
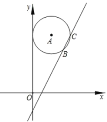
【题目】已知,点A为⊙0外一点,过A作⊙O的切线与⊙O相切于点P,连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA。
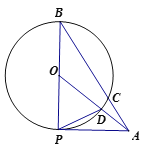
(1)求证:PO=PD
(2)若AC=![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)见解析;(2)半径![]() .
.
【解析】
(1)设∠OAP=∠DPA=x,根据三角形外角的性质和切线的性质,分别表示出∠ODP和∠OPD,根据∠OPD=∠ODP可求出x=30°,易得△ODP是等边三角形,结论得证;
(2)设半径为r,则AP=![]() ,然后用勾股定理求得
,然后用勾股定理求得![]() ,最后根据切割线定理列出方程求解即可.
,最后根据切割线定理列出方程求解即可.
解:(1)设∠OAP=∠DPA=x,则∠ODP=2x,
∵PA为切线,
∴∠OPA=90°,
∴∠OPD=90°-x,
∵∠OPD=∠ODP,
∴90°-x=2x,
解得:x=30°,
∴∠ODP=∠OPD=90°-x=60°,
∴△ODP是等边三角形,
∴PO=PD;
(2)设半径为r,
由(1)得∠OAP=30°,
∴AP=![]() ,
,
∴![]() ,
,
由切割线定理可得:AP2=AC·AB,即![]() ,
,
解得:![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下.
(1)补全下表,在所给坐标系中画出函数的图象:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | … |
(2)观察图象,写出该函数两条不同类型的性质;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根,a的取值范围是 .