题目内容
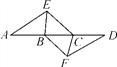
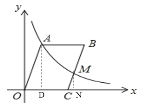
【题目】如图，OABC的周长为14，∠AOC=60°，以O为原点，OC所在直线为x轴建立直角坐标系，函数y
（x＞0）的图象经过OABC的顶点A和BC的中点M，则k的值为（ ）
A.2
B.4C.6D.12
【答案】B
【解析】
设OA=a，OC=b，找出a，b的关系，作AD⊥x轴于D，MN⊥x轴于N，分别表示出CD和AD，从而得出A点的坐标，根据题目条件表示出M点的坐标，代入解析式列出方程即可求解．
解：设OA=a，OC=b
∵四边形OABC的周长为14
∴a+b=7，
∴b=7-a，
作AD⊥x轴于D，MN⊥x轴于N
∵∠AOC=60°
∴OD
a，AD
a
∴A（
a，
a）
∵M是BC的中点
∴CN
a，MN
a
∴M（7-a
a，
a）
∴a×a=（7-aa）×（a）
解得：a=4
∴A（2，2
）
∴k=2
4
故选：B．
练习册系列答案
出彩同步大试卷系列答案
相关题目
