题目内容
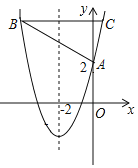
【题目】如图是某同学对一道作业题的解题思路,课堂上师生据此展开了讨论.问题如图,已知A(1,![]() )、B(4,0),∠OAB的平分线AC交x轴于点C,求OC的长.思路:作AD⊥OB,CE⊥AB,CF⊥OA
)、B(4,0),∠OAB的平分线AC交x轴于点C,求OC的长.思路:作AD⊥OB,CE⊥AB,CF⊥OA
①A坐标→OD=1,AD=![]() ,OA=2→∠AOC=60°;
,OA=2→∠AOC=60°;
②A、B坐标→OA=2,OB=4,AB=2![]() →∠OAB=90°;
→∠OAB=90°;
③AC平分∠OAB→CE=CF;
④S△AOC+S△ABC=S△AOB→AOCF+ABCE=OAAB→CF=3﹣![]() ;
;
⑤综上,Rt△OCF中,OC=![]() ﹣2.可以优化吗?
﹣2.可以优化吗?
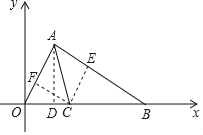
(1)同学们发现不需要证“∠OAB=90°”也能求解,简要说明理由.几位同学提出了不同的思路
①甲说:S△AOC和S△ABC的面积之比既是![]() ,又是
,又是![]() ,从而
,从而![]() ;
;
②乙说:在AB边上取点G,使AG=AO,连接CG,可知BG的长即为所求;
③丙说:延长AC交△AOB的外接圆于N,再利用一次函数或相似求出OC.
请你选择其中一种解法,利用图2和已有步骤完成解答.有什么收获?
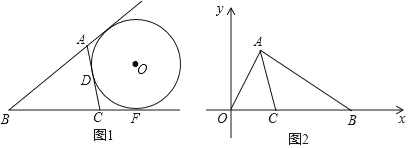
(2)面积法是图形问题中确定数量关系的有效方法,请利用面积法求解:如图1,⊙O与△ABC的边AC,边BA、BC的延长线AE、CF相切,切点分别为D、E、F.设△ABC的面积为S,BC=a,AC=b,AB=c,请用含S、a、b、c的式子表示⊙O的半径R,直接写出结果.
【答案】(1)方法可以优化.见解析。本题收获:学会了利用面积法解决问题,学会构建一次函数,利用数形结合的思想解决问题.
(2)R=![]() .
.
【解析】
(1)根据甲、乙、丙的三种思路解决问题即可;
(2)根据S△ABC=S△AOB+S△OBC﹣S△AOC,利用面积法解决问题即可.
解:(1)方法可以优化.
方法一:如图2﹣1中,作CE⊥OA于E,CF⊥AB于F.
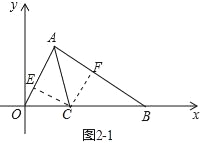
∵CA平分∠OAB,CE⊥OA,CF⊥AB,
∴CE=CF,
∵![]() =
=![]()
![]() =
=![]() =
=![]() ,
,
∴OC=OB![]() =2
=2![]() ﹣2.
﹣2.
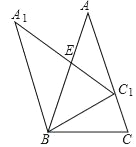
方法二:如图2﹣2中,在AB边上取点G,使AG=AO,连接CG.
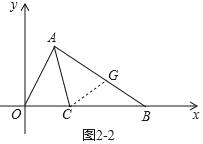
∵AO=AG,∠OAC=∠CAG,AC=AC,
∴△ACO≌△ACG(SAS),
∴OC=CG,
∵∠AOC=∠AGC=60°,∠ABO=30°,∠AGC=∠GCB+∠ABO,
∴∠GCB=∠GBC,
∴GC=GB,
∴OC=GB=2![]() ﹣2.
﹣2.
方法三:如图2﹣3中,延长AC交△ABC的外接圆于点N,连接ON,BN.
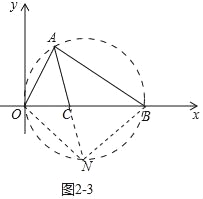
易知N(2,﹣2),
∵A(1,![]() ),
),
∴直线AN的解析式为y=(﹣2﹣![]() )x+2
)x+2![]() +2,
+2,
令y=0,得到x=2![]() ﹣2,
﹣2,
∴C(2![]() ﹣2),
﹣2),
∴OC=2![]() ﹣2.
﹣2.
本题收获:学会了利用面积法解决问题,学会构建一次函数,利用数形结合的思想解决问题.
(2)如图1中,连接OB,OE,OD,OF.
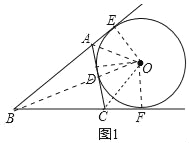
∵⊙O与△ABC的边AC,边BA、BC的延长线AE、CF相切,切点分别为D、E、F,
∴OE⊥AB,OD⊥AC,OF⊥BC,
∵S△ABC=S△AOB+S△OBC﹣S△AOC,
∴S=![]() cR+
cR+![]() aR﹣
aR﹣![]() bR,
bR,
∴R=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案