题目内容
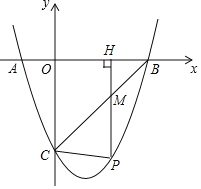
【题目】如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=﹣2，平行于x轴的直线与抛物线交于B、C两点，点B在对称轴左侧，BC=6．
（1）求此抛物线的解析式．
（2）点P在x轴上，直线CP将△ABC面积分成2：3两部分，请直接写出P点坐标．
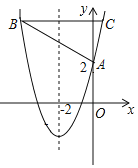
【答案】（1）抛物线的解析式为y=x2+4x+2；（2）P的坐标为（﹣6，0）或（﹣13，0）．
【解析】（1）由对称轴直线x=2，以及A点坐标确定出b与c的值，即可求出抛物线解析式；
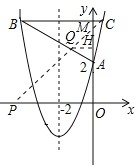
（2）由抛物线的对称轴及BC的长，确定出B与C的横坐标，代入抛物线解析式求出纵坐标，确定出B与C坐标，利用待定系数法求出直线AB解析式，作出直线CP，与AB交于点Q，过Q作QH⊥y轴，与y轴交于点H，BC与y轴交于点M，由已知面积之比求出QH的长，确定出Q横坐标，代入直线AB解析式求出纵坐标，确定出Q坐标，再利用待定系数法求出直线CQ解析式，即可确定出P的坐标．
（1）由题意得：x=﹣
=﹣
=﹣2，c=2，
解得：b=4，c=2，
则此抛物线的解析式为y=x2+4x+2；
（2）∵抛物线对称轴为直线x=﹣2，BC=6，
∴B横坐标为﹣5，C横坐标为1，
把x=1代入抛物线解析式得：y=7，
∴B（﹣5，7），C（1，7），
设直线AB解析式为y=kx+2，
把B坐标代入得：k=﹣1，即y=﹣x+2，
作出直线CP，与AB交于点Q，过Q作QH⊥y轴，与y轴交于点H，BC与y轴交于点M，
可得△AQH∽△ABM，
∴
，
∵点P在x轴上，直线CP将△ABC面积分成2：3两部分，
∴AQ：QB=2：3或AQ：QB=3：2，即AQ：AB=2：5或AQ：QB=3：5，
∵BM=5，
∴QH=2或QH=3，
当QH=2时，把x=﹣2代入直线AB解析式得：y=4，
此时Q（﹣2，4），直线CQ解析式为y=x+6，令y=0，得到x=﹣6，即P（﹣6，0）；
当QH=3时，把x=﹣3代入直线AB解析式得：y=5，
此时Q（﹣3，5），直线CQ解析式为y=
x+
，令y=0，得到x=﹣13，此时P（﹣13，0），
综上，P的坐标为（﹣6，0）或（﹣13，0）．
