��Ŀ����
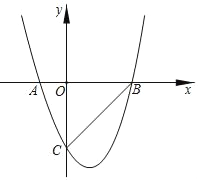
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+b��k��0����������y��ax2��4ax+3a�ĶԳ��ύ�ڵ�A��m����1������A����x��ĶԳƵ�ǡΪ�����ߵĶ��㣮
��1���������ߵĶԳ��ἰa��ֵ��
��2���ᡢ�����궼�������ĵ�������㣮��ֱ��y��kx+b��k��0����������Χ�ɵķ���������߽磩ΪW��
����k��1ʱ��ֱ��д������W�ڵ����������
��������W��ǡ��3�����㣬��Ϻ���ͼ����b��ȡֵ��Χ��
���𰸡���1��![]() ��
��![]() ����2����2����
����2����2����![]() ��
��![]() .
.
��������
��1��������![]() ����Ϊ����ʽ����Գ���x=2�붥�����꣨2,1�������뼴����a����2����ͼ��ʾ���ٵ�
����Ϊ����ʽ����Գ���x=2�붥�����꣨2,1�������뼴����a����2����ͼ��ʾ���ٵ�![]() ʱ������
ʱ������![]() �ڵ��������Ϊ2������
�ڵ��������Ϊ2������![]() ����ֱ�߹�
����ֱ�߹�![]() ��
��![]() �������
�������![]() ��
��![]() ���ֱ������bֵ���������ȡֵ��Χ����
���ֱ������bֵ���������ȡֵ��Χ����![]() ���ɶԳ��Կɵ�b��ȡֵ��Χ.
���ɶԳ��Կɵ�b��ȡֵ��Χ.
��![]() ��ȡֵ��Χ�ǣ�
��ȡֵ��Χ�ǣ�![]() ��
��![]() ��
��
�⣺��1�����εã�![]() .
.
��Գ���Ϊ![]() ��
��
���![]() ������Ϊ
������Ϊ![]() �ɵ������߶���Ϊ
�ɵ������߶���Ϊ![]()
�ѵ�![]() ������������߿ɵã�
������������߿ɵã�![]() ��
��

��2���ٵ�![]() ʱ������
ʱ������![]() �ڵ��������Ϊ2����
�ڵ��������Ϊ2����
����![]() ��
��
��ֱ�߹�![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��ֱ�߹�![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
�ɶԳ��Կɵã�![]() ��
��
��![]() ��ȡֵ��Χ�ǣ�
��ȡֵ��Χ�ǣ�![]() ��
��![]() ��
��

��ϰ��ϵ�д�
�����Ŀ