题目内容
【题目】如图,在△ABC中,AB=AC,∠C=72°,△ABC绕点B逆时针旋转,当点C的对应点C1落在边AC上时,设AC的对应边A1C1与AB的交点为E,则∠BEC1=___°.
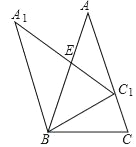
【答案】72
【解析】
根据等腰三角形的性质得到∠ABC=∠C=72°,根据三角形的内角和得到∠CBC1=180°﹣72°﹣72°=36°,求得∠ABC1=72°﹣36°=36°,根据旋转的性质得到∠A1C1B=∠C=72°,于是得到结论.
∵AB=AC,∠C=72°,
∴∠ABC=∠C=72°,
∴∠CBC1=180°﹣72°﹣72°=36°,
∴∠ABC1=72°﹣36°=36°,
∵△ABC绕点B逆时针旋转得到△A1BC1,
∴A1C1B=∠C=72°,
∴∠BEC1=72°,
故答案为:72.

练习册系列答案
相关题目