ЬтФПФкШн
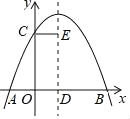
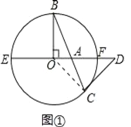
ЁОЬтФПЁПЭЌбЇУЧЖМбЇЯАЙ§ЁЖМИКЮЁЗПЮБОЕкШ§ВсЕк199вГЕФЕк11ЬтЃЌЫќЪЧетбљЕФЃКШчЭМЃЌAЮЊЁбOЕФжБОЖEFЩЯЕФвЛЕуЃЌOBЪЧКЭетЬѕжБОЖДЙжБЕФАыОЖЃЌBAКЭЁбOЯрНЛгкСэвЛЕуCЃЌЙ§ЕуCЕФЧаЯпКЭEFЕФбгГЄЯпЯрНЛгкЕуDЃЌЧѓжЄЃКDAЃНDCЃЎ

ЃЈ1ЃЉЯжНЋЭМ1жаЕФжБОЖEFЫљдкжБЯпНјааЦНаавЦЖЏЕНЭМ2ЫљЪОЕФЮЛжУЃЌДЫЪБOBгыEFДЙжБЯрНЛгкHЃЌЦфЫќЬѕМўВЛБфЃЎ
ЂйЧѓжЄЃКDAЃНDCЃЛ
ЂкЕБDFЃКEFЃН1ЃК8ЃЌЧвDFЃН![]() ЪБЃЌЧѓABACЕФжЕЃЎ
ЪБЃЌЧѓABACЕФжЕЃЎ
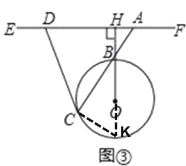
ЃЈ2ЃЉНЋЭМ2жаЕФEFЫљдкжБЯпМЬајЯђЩЯЦНаавЦЖЏЕНЭМ3ЫљЪОЕФЮЛжУЃЌЪЙEFгыOBЕФбгГЄЯпДЙжБЯрНЛгкHЃЌAЮЊEFЩЯвьгкHЕФвЛЕуЃЌЧвAHаЁгкЁбOЕФЧаЯпНЛEFгкDЃЌЪдВТЯыЃКDAЃНDCЪЧЗёШдШЛГЩСЂЃПжЄУїФуЕФНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйМћНтЮіЂк24ЃЈ2ЃЉНсТлDAЃНDCШдШЛГЩСЂ
ЁОНтЮіЁП
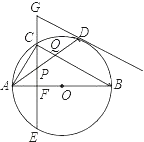
ЃЈ1ЃЉЂйСЌНгOCЃЌРћгУЧаЯпЕФаджЪдђПЩЕУЕНOCЁЭDCЃЌШЛКѓЕУЕНЁЯDCA=90Ёу-ЁЯACO=90Ёу-ЁЯB=ЁЯDACЃЌРћгУЕШНЧЖдЕШБпЕУЕНDA=DCМДПЩЃЛ
ЂкРћгУDFЃКEF=1ЃК8ЃЌDF=![]() дђПЩЕУЕНEF=8DF=8
дђПЩЕУЕНEF=8DF=8![]() ЃЌШЛКѓРћгУЧаЯпГЄЖЈРэЧѓЕУDCЕФГЄЃЌНјЖјЕУЕНDCЁЂADЕФГЄЃЌШЛКѓРћгУЧаЯпГЄЖЈРэЕУЃКABAC=AEAF=24ЃЛ
ЃЌШЛКѓРћгУЧаЯпГЄЖЈРэЧѓЕУDCЕФГЄЃЌНјЖјЕУЕНDCЁЂADЕФГЄЃЌШЛКѓРћгУЧаЯпГЄЖЈРэЕУЃКABAC=AEAF=24ЃЛ
ЃЈ2ЃЉНсТлШдШЛГЩСЂЃЌбгГЄBOНЛЁбOгкKЃЌСЌCKЃЌРћгУЧаЯпЕФаджЪПЩвдЕУЕНЁЯDCA=ЁЯCKB=90Ёу-ЁЯCBKЃЌДгЖјЕУЕНЁЯDCA=ЁЯBAHЃЌЮЪЬтЕУжЄ.
ЃЈ1ЃЉЂйжЄУїЃКСЌOCЃЌдђOCЁЭDCЃЌ
ЁрЁЯDCAЃН90ЁуЉЁЯACOЃН90ЁуЉЁЯBЃЌ
гжЁЯDACЃНЁЯBAEЃН90ЁуЉЁЯBЃЌ
ЁрЁЯDACЃНЁЯDCAЁрDAЃНDCЃЌ
ЂкЁпDFЃКEFЃН1ЃК8ЃЌDFЃН![]() ЃЌ
ЃЌ
ЁрEFЃН8DFЃН8![]() ЃЌ
ЃЌ
гжDCЮЊЧаЯпЃЌ
ЁрDC2ЃНDFDEЃН![]() ЁС9
ЁС9![]() ЃН18ЃЌ
ЃН18ЃЌ
ЁрDCЃН3![]() ЃЌ
ЃЌ
ЁрADЃНDCЃН3![]() ЃЌ
ЃЌ
ЁрAFЃНADЉDFЃН2![]() ЃЌ
ЃЌ
ЁрAEЃНEFЉAFЃН6![]() ЃЌ
ЃЌ
ЁрABACЃНAEAFЃН24ЃЛ
ЃЈ2ЃЉНсТлDAЃНDCШдШЛГЩСЂЃЌРэгЩШчЯТЃК
бгГЄBOНЛЁбOгкKЃЌСЌCKЃЌдђЁЯKCBЃН90ЁуЃЌ
гжDCЮЊЁбOЕФЧаЯпЃЌ
ЁрЁЯDCAЃНЁЯCKBЃН90ЁуЉЁЯCBKЃЌ
гжЁЯBAHЃН90ЁуЉЁЯHBAЃЌ
ЖјЁЯCBKЃНЁЯHBAЃЌ
ЁрЁЯDCAЃНЁЯBAHЃЌ
ЁрDAЃНDCЃЎ

ЁОЬтФПЁПФГДѓбЇЩњРћгУЪюМй40ЬьЩчЛсЪЕМљВЮгыСЫвЛМвЭјЕъОгЊЃЌСЫНтЕНвЛжжГЩБОЮЊ20дЊ/МўЕФаТаЭЩЬЦЗдкЕкxЬьЯњЪлЕФЯрЙиаХЯЂШчЯТБэЫљЪОЁЃ
ЯњЪлСПpЃЈМўЃЉ | P=50ЁЊx |
| ЕБ1ЁмxЁм20ЪБЃЌ |
ЃЈ1ЃЉЧыМЦЫуЕкМИЬьИУЩЬЦЗЕФЯњЪлЕЅМлЮЊ35дЊ/МўЃП
ЃЈ2ЃЉЧѓИУЭјЕъЕкxЬьЛёЕУЕФРћШѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЁЃ
ЃЈ3ЃЉет40ЬьжаИУЭјЕъЕкМИЬьЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП