Question

【题目】在平面直角坐标系中，抛物线﹔与轴交于点，抛物线的顶点为，直线．

(1)当时，画出直线和抛物线，并直接写出直线被抛物线截得的线段长．

(2)随着取值的变化，判断点是否都在直线上并说明理由．

(3)若直线被抛物线截得的线段长不小于3，结合函数的图像，直接写出的取值范围．

Answer 1

【答案】（1）图详见详解，；（2）无论取何值，点都在直线上，理由见详解；（3）或．

【解析】

（1）当时，抛物线的函数表达式为，直线的函数表达式为,画出图像即可.

（2）先求出C、D两点坐标，再代入直线的解析式进行检验.

（3）联立直线与抛物线解析式求出交点坐标，再根据两点间距离不小于3列出不等式求解即可.

解：（1）当时，抛物线的函数表达式为，直线的函数表达式为

画出的两个函数的图像如图所示：

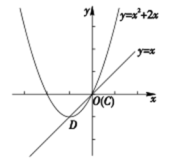
联立函数解析式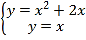 解得

∴直线被抛物线截得的线段长为：

(2)∵抛物线与轴交于点，

∴点的坐标为．

∵，

∴抛物线的顶点的坐标为．

对于直线：

当时，；

当时，．

∴无论取何值，点都在直线上．

(3)由（2）知，直线与抛物线的交点为：

∴

解得或

∴的取值范围是或