Question

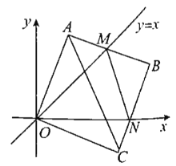
【题目】如图，直线PA是一次函数的图象，直线PB是一次函数的图象，若PA与轴交于点Q，且，则的值分别是（ ）

A.B.2,1C.D.

Answer 1

【答案】B

【解析】

由题意可求得点A，B，Q的坐标，然后联立y＝x＋n与y＝2x＋m，即可求得点P的坐标，由S四边形PQOB＝，AB＝2，可得：m＋2n＝4，S△PABS△AOQ＝×2×n·n＝＝，即可求得m与n的值．

解：由题意得：点A的坐标为（n，0），点Q的坐标为（0，n），点B的坐标为（，0），

∵点P是PA与PB的交点，

∴联立 ，

解得：，

∴点P的坐标为：（，），

∵AB＝2，

∴OA＋OB＝n＋＝＝2，

∴m＋2n＝4，

∵S四边形PQOB＝，

∴S△PABS△AOQ＝×2×n·n＝＝，

解得：n＝1（舍去负值），

∴m＝2．

故选：B．