题目内容
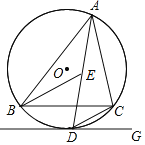
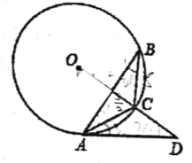
【题目】如图,![]() 内接于
内接于![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() .
.
(1)求证;![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见详解;(2)![]()
【解析】
(1)连接OA,由圆周角定理得∠AOC=60°,则△OAC为等边三角形,则OA⊥AD,得到∠D=30°,即可得到结论成立;
(2)由![]() ,得到∠BAC=30°,则CD=AC=BC=5,然后得到半径OA=OC=5,根据勾股定理,即可求出AD的长度.
,得到∠BAC=30°,则CD=AC=BC=5,然后得到半径OA=OC=5,根据勾股定理,即可求出AD的长度.
解:(1)如图,连接OA,
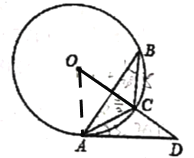
∵![]() ,
,
∴![]() ,
,
∴△AOC是等边三角形,
∴OA=OC=AC,∠OAC=60°,
∵![]() ,
,
∴∠OAD=90°,
∴∠D=30°,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴∠BAD+∠D=90°,
∴∠BAD=60°,
∵![]() ,
,
∴∠BAC=30°=∠B,
∴AC=BC=CD=5,
∴OA=OC=AC=5,
∴OD=10,
在Rt△OAD中,由勾股定理,得
![]() .
.

练习册系列答案
相关题目