��Ŀ����
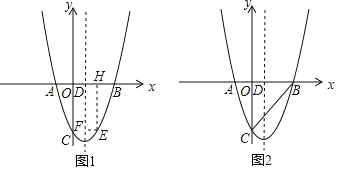
����Ŀ����ͼ��������y=x2��4x��5��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C�������ߵĶԳ�����x�ύ�ڵ�D��
��1����A��B��C��������꼰�����ߵĶԳ��ᣮ
��2����ͼ1����E��m��n��Ϊ��������һ�㣬��2��m��5������E��EF��x�ᣬ�������ߵĶԳ����ڵ�F����EH��x���ڵ�H�����ı���EHDF�ܳ������ֵ��
��3����ͼ2����PΪ�����߶Գ�����һ�㣬�Ƿ���ڵ�P��ʹ�Ե�P��B��CΪ�������������ֱ�������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A����1��0����B��5��0����C��0����5����x=2����2��![]() ����3�����ڣ���P������Ϊ��2��3����2����7����2����6����2��1����
����3�����ڣ���P������Ϊ��2��3����2����7����2����6����2��1����
��������
��1���ֱ���x=0��y=0���������ߵĽ���ʽ�У��ɵ�A��B��C�����꣬���ݶԳ�
�ԣ��ɵöԳ��
��2�����ݾ����ܳ���ʽ��ʾ�ı���EHDF�ܳ��������ݶ��κ����Ķ���ʽ�ɵ��ı���EHDF
�ܳ������ֵ��
��3�������������
�ٵ���CBP=90��ʱ����ͼ2��������PDB�ס�BOC���б���ʽ�ã�PD=DB���ɵý��ۣ�
�ڵ���BCP=90��ʱ����ͼ3��������PCG�ס�BDG����![]() =
=![]() ���ɵ�PG�ij����Ӷ�д��P
���ɵ�PG�ij����Ӷ�д��P
�����ꣻ
����ABΪֱ����Բ�����Գ�����P1��P2����ͼ4��������P1DB�ס�CHP1����![]() ��
��
�з��̿ɵý��ۣ�
�⣺��1����x=0ʱ��y=��5��
��C��0����5����
��y=0ʱ��x2��4x��5=0��
x1=5��x2=��1��
��A����1��0����B��5��0����
�ɶԳ��Եã������ߵĶԳ����ǣ�![]()
��2����ͼ1����E��m��n������2��m��5��
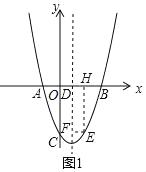
��E�ڵ������ޣ�
��EF=m��2��EH=n=��m2+4m+5��
���ı���EHDF�ܳ�ΪW��
��W=2��EF+EH��=2��m��2��m2+4m+5��=��2m2+10m+6![]()
�ߩ�2��0��
�൱![]() ʱ���ı���EHDF�ܳ������ֵ��
ʱ���ı���EHDF�ܳ������ֵ��![]() ��
��
��3����P��2��y����
�����������
�ٵ���CBP=90��ʱ����ͼ2��
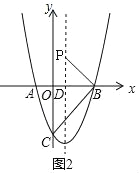
���PBO=��OCB��
�ߡ�PDB=��COB=90����
���PDB�ס�BOC��
��![]()
��PD=DB��
��y=5��2=3��
��P��2��3����
�ڵ���BCP=90��ʱ����ͼ3��
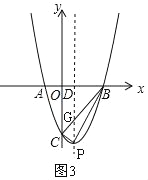
�ߡ�OBC=45����
���GDB�ǵ���ֱ�������Σ�
��BD=DG=3��
��![]()
��![]()
��![]()
�ߡ�PCG�ס�BDG��
��![]()
��![]()
��PG=4��
��P��2����7����
����ABΪֱ����Բ�����Գ�����P1��P2����ͼ4�����CP1B=��CP2B=90����
��C��CH�ͶԳ�����H��
���P1DB�ס�CHP1��
��![]() ,
,
��![]()
��y1=��6���ᣩ��y2=1��
��P1��2��1����
ͬ���ã�P2��2����6����
������������P��������2��3����2����7����2����6����2��1����

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�����Ŀ��ij��������֯������ʵʮ�Ŵ��������λ���ж�����ʦ�ݽ����������ݸ�У�����ɼ���Сѧ�顢��ѧ��ֱ�ѡ��10����ʦ�μӾ�������Щѡ�ֵľ����ɼ���ͼ��ʾ��
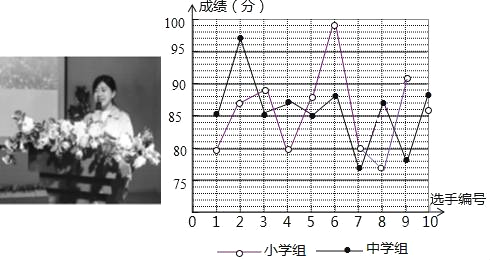
������ͼ�ṩ����Ϣ���ش��������⣺
��1���������������������
����ɼ� | ���� | ƽ���� | ���� |
Сѧ�� | ���� | 85.7 | 39.6 |
��ѧ�� | 85 | ���� | 27.8 |
��2������ƽ�����뷽�����Ϊ�ĸ��������ɼ�����Щ����˵�����ɣ�
��3������ÿ��ľ���ѡ���зֱ�ѡ��3�˲μ��ܾ���������Ϊ�ĸ����ʤ�Ŀ����Դ�Щ����˵�����ɣ�