题目内容
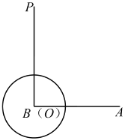
【题目】如图，已知射线
，点
从B点出发，以每秒1个单位长度沿射线
向右运动；同时射线
绕点
顺时针旋转一周，当射线停止运动时，点随之停止运动.以为圆心，1个单位长度为半径画圆，若运动两秒后，射线与
恰好有且只有一个公共点，则射线旋转的速度为每秒______度.
【答案】30或60
【解析】
射线
与
恰好有且只有一个公共点就是射线与相切，分两种情况画出图形，利用圆的切线的性质和30°角的直角三角形的性质求出旋转角，然后根据旋转速度=旋转的度数÷时间即得答案.
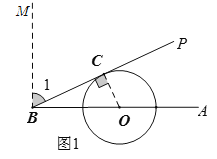
解：如图1，当射线与在射线BA上方相切时，符合题意，设切点为C，连接OC，则OC⊥BP，
于是，在直角△BOC中，∵BO=2，OC=1，∴∠OBC=30°，∴∠1=60°，
此时射线旋转的速度为每秒60°÷2=30°；
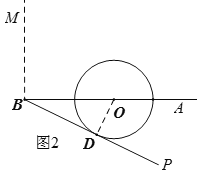
如图2，当射线与在射线BA下方相切时，也符合题意，设切点为D，连接OD，则OD⊥BP，
于是，在直角△BOD中，∵BO=2，OD=1，∴∠OBD=30°，∴∠MBP=120°，
此时射线旋转的速度为每秒120°÷2=60°；
故答案为：30或60.
练习册系列答案
相关题目
