ЬтФПФкШн
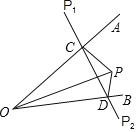
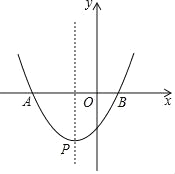
ЁОЬтФПЁПдквдЕуOЮЊдЕуЕФЦНУцжБНЧзјБъЯЕжаЃЌБпГЄЮЊ1ЕФе§ЗНаЮOABCЕФСНЖЅЕуAЃЌCЗжБ№дкyжсЃЌ![]() жсЕФе§АыжсЩЯЃЌЯжНЋе§ЗНаЮOABCШЦЕуЇАЫГЪБеыа§зЊЃЌЕБЕуAЕквЛДЮТфдкжБЯп
жсЕФе§АыжсЩЯЃЌЯжНЋе§ЗНаЮOABCШЦЕуЇАЫГЪБеыа§зЊЃЌЕБЕуAЕквЛДЮТфдкжБЯп![]() ЩЯЪБЃЌЭЃжЙзЊЖЏЃЌа§зЊЙ§ГЬжаЃЌABБпНЛжБЯп
ЩЯЪБЃЌЭЃжЙзЊЖЏЃЌа§зЊЙ§ГЬжаЃЌABБпНЛжБЯп![]() гкЕуMЃЌBCБпНЛжсгкЕуNЃЎ
гкЕуMЃЌBCБпНЛжсгкЕуNЃЎ
ЃЈ1ЃЉа§зЊЭЃжЙЪБе§ЗНаЮа§зЊЕФЖШЪ§ЪЧ_________.
ЃЈ2ЃЉдка§зЊЙ§ГЬжаЃЌЕБMNКЭACЦНааЪБЃЌ
Ђй![]() гы
гы![]() ЪЧЗёШЋЕШЃПДЫЪБе§ЗНаЮOABCа§зЊЕФЖШЪ§ЪЧЖрЩйЃП
ЪЧЗёШЋЕШЃПДЫЪБе§ЗНаЮOABCа§зЊЕФЖШЪ§ЪЧЖрЩйЃП
ЂкжБНгаДГі![]() ЕФжмГЄЕФжЕЃЌВЂХаЖЯетИіжЕдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаЪЧЗёЗЂЩњБфЛЏЃЎ
ЕФжмГЄЕФжЕЃЌВЂХаЖЯетИіжЕдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаЪЧЗёЗЂЩњБфЛЏЃЎ
ЁОД№АИЁПЃЈ1ЃЉ45ЁуЃЛЃЈ2ЃЉЂйШЋЕШЃЛ22.5ЁуЃЛЂк![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаЃЌ
ЃЌдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаЃЌ![]() ЕФжмГЄВЛЗЂЩњБфЛЏЃЎ
ЕФжмГЄВЛЗЂЩњБфЛЏЃЎ
ЁОНтЮіЁП
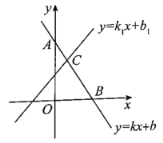
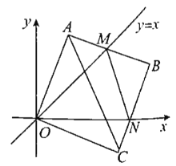
ЃЈ1ЃЉИљОнжБЯпy=xЭМЯѓЩЯЕуЕФЬиЕуЃЌЕУГіЯпy=xгыyжсЕФМаНЧЪЧ45ЁуЃЌМДПЩЕУГіЧѓЕУБпOAа§зЊЕФНЧЖШЃЛ
ЃЈ2ЃЉЂйРћгУSASЕУГіШЋЕШЃЌИљОне§ЗНаЮвЛИіФкНЧЕФЖШЪ§ЧѓГіЁЯAOMЕФЖШЪ§ЃЌМДПЩЕУГіД№АИЃЛ
ЂкРћгУШЋЕШАбЁїMBNЕФИїБпећРэЕНГЩгые§ЗНаЮЕФБпГЄгаЙиЕФЪНзгМДПЩЃЎ
ЃЈ1ЃЉЁпAЕуЕквЛДЮТфдкжБЯп![]() ЩЯЪБЭЃжЙа§зЊЃЌжБЯп
ЩЯЪБЭЃжЙа§зЊЃЌжБЯп![]() гыyжсЕФМаНЧЪЧ
гыyжсЕФМаНЧЪЧ![]() ЃЌ
ЃЌ
Ёр![]() а§зЊСЫ45ЁуЃЛ
а§зЊСЫ45ЁуЃЛ
ЃЈ2ЃЉЂйЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёпдк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ
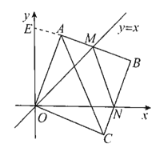
Ёра§зЊЙ§ГЬжаЃЌЕБMNКЭACЦНааЪБЃЌе§ЗНаЮOABCа§зЊЕФЖШЪ§ЮЊ![]() ЃЎ
ЃЎ
Ђк![]() ЕФжмГЄЕФжЕЮЊ2ЃЌЧвдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаВЛЗЂЩњБфЛЏЃЎ
ЕФжмГЄЕФжЕЮЊ2ЃЌЧвдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаВЛЗЂЩњБфЛЏЃЎ
РэгЩШчЯТЃКШчЭМЫљЪОЃЌбгГЄBAНЛyжсгкЕуEЃЌ
дђ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
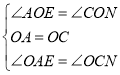
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
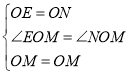 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЎ
ЃЎ
Ёрдке§ЗНаЮOABCЕФа§зЊЙ§ГЬжаЃЌ![]() ЕФжмГЄВЛЗЂЩњБфЛЏЃЎ
ЕФжмГЄВЛЗЂЩњБфЛЏЃЎ

 гЅХЩНЬИЈЯЮНгНЬВФКгББНЬг§ГіАцЩчЯЕСаД№АИ
гЅХЩНЬИЈЯЮНгНЬВФКгББНЬг§ГіАцЩчЯЕСаД№АИ ГѕжаЪюЦкЯЮНгЯЕСаД№АИ
ГѕжаЪюЦкЯЮНгЯЕСаД№АИЁОЬтФПЁПАЫЃЈ1ЃЉАрЮхЮЛЭЌбЇВЮМгбЇаЃОйАьЕФЪ§бЇОКШќЃЌЪдОэжаЙВга20ЕРЬтЃЌЙцЖЈУПЬтД№ЖдЕУ5ЗжЃЌД№ДэПл2ЗжЃЌЮДД№ЕУ0ЗжЁЃШќКѓAЃЌBЃЌ CЃЌDЃЌEЮхЮЛЭЌбЇЖдееЦРЗжБъзМЛивфВЂМЧТМСЫздМКЕФД№ЬтЧщПіЃЈEЭЌбЇжЛМЧЕУга7ЕРЬтЮДД№ЃЉЃЌОпЬхШчЯТБэЃК
ВЮШќЭЌбЇ | Д№ЖдЬтЪ§ | Д№ДэЬтЪ§ | ЮДД№ЬтЪ§ |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
ЃЈ1ЃЉИљОнвдЩЯаХЯЂЃЌЧѓAЃЌBЃЌCЃЌDЫФЮЛЭЌбЇГЩМЈЕФЦНОљЗжЃЛ
ЃЈ2ЃЉзюКѓЛёжЊЃКAЃЌBЃЌCЃЌDЃЌEЮхЮЛЭЌбЇГЩМЈЗжБ№ЪЧ95ЗжЃЌ81ЗжЃЌ64ЗжЃЌ83ЗжЃЌ58Зж.
ЂйЧѓEЭЌбЇЕФД№ЖдЬтЪ§КЭД№ДэЬтЪ§ЃЛ
ЂкОМЦЫуЃЌAЃЌBЃЌCЃЌDЫФЮЛЭЌбЇЪЕМЪГЩМЈЦНОљЗжЪЧ80.75ЗжЃЌгыЃЈ1ЃЉжаЫуЕУЕФЦНОљЗжВЛЯрЗћЃЌЗЂЯжЪЧЦфжавЛЮЛЭЌбЇМЧДэСЫздМКЕФД№ЬтЧщПі.ЧыжИГіФФЮЛЭЌбЇМЧДэСЫЃЌВЂаДГіЫћЕФЪЕМЪД№ЬтЧщПіЃЈжБНгаДГіД№АИМДПЩЃЉ.