题目内容
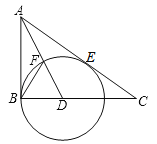
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)设![]() 与
与![]() 切于点
切于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
②当![]() __________时,
__________时,![]() 为等腰三角形.
为等腰三角形.
【答案】(1)见解析;(2)①30°;②1+![]()
【解析】
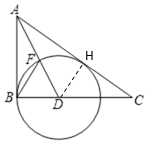
(1)过点D作DH⊥AC于点H,根据角平分线的性质得到DH=BD即可得到结论;
(2)①根据菱形的性质证得△BDF是等边三角形,即可求出答案;
②根据等腰直角三角形的性质得到CD=1,利用勾股定理求出CD=![]() ,设AB=x,由勾股定理建立方程求出x即可得到答案.
,设AB=x,由勾股定理建立方程求出x即可得到答案.
(1)过点D作DH⊥AC于点H,
∵![]() ,
,
∴DB⊥AB,
∵AD平分∠BAC,
∴DH=BD,
∴DH是![]() 的半径,
的半径,
∴![]() 是
是![]() 的切线.
的切线.
(2)①∵四边形![]() 为菱形,
为菱形,
∴BF=EF=DE=BD,
∵DF=DB=DE,
∴DF=DB=BF,
∴△BDF是等边三角形,
∴∠BDF=60°,
∵![]() ,
,
∴∠BAD=30°,
故答案为:30°;
②∵![]() 与
与![]() 切于点
切于点![]() ,
,
∴∠AED=90°,
∵![]() 为等腰三角形,
为等腰三角形,
∴CE=DE=![]() ,
,
∴CD=![]() ,
,
设AB=x,则AE=x,AC=x+1,BC=1+![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得x=1+![]() ,
,
故答案为:1+![]() .
.


练习册系列答案
相关题目