题目内容
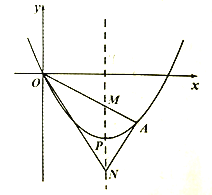
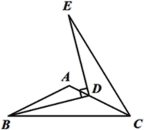
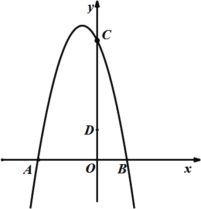
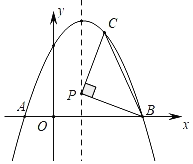
【题目】如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+3经过点A(﹣1，0)和点B(3，0)，该抛物线对称轴上的点P在x轴上方，线段PB绕着点P逆时针旋转90°至PC（点B对应点C），点C恰好落在抛物线上．
（1）求抛物线的表达式并写出抛物线的对称轴；
（2）求点P的坐标；
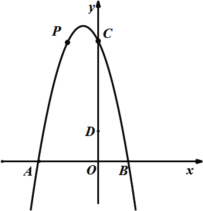
（3）点Q在抛物线上，联结AC，如果∠QAC＝∠ABC，求点Q的坐标．
【答案】（1）y＝﹣x2+2x+3，x＝1；（2）(1，1)；（3）(
，﹣
)
【解析】
（1）将点A、B坐标代入抛物线表达式，即可求解；
（2）证明△PMC≌△BNP（AAS），则PM＝BN，MC＝PN，即可求解；
（3）设MH＝3x，用x表示AM、GM，利用AG＝AM+GM＝
，求出x的值；在△AOH中，OH＝
，求得点H的坐标，即可求解．
（1）将点A、B坐标代入抛物线表达式得：
，解得：
，
故抛物线的表达式为：y＝﹣x2+2x+3①；
函数的对称轴为：x＝1；
（2）设点C（m，n），则n＝﹣m2+2m+3，点P（1，s），
如图1，设抛物线对称轴交x轴于点N，过点C作CM⊥PN交抛物线对称轴于点M，
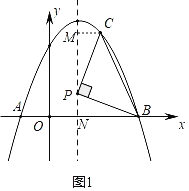
∵∠PBN+∠BPN＝90°，∠BPN+∠MPC＝90°，
∴∠MPC＝∠PBN，
∵∠PMC＝∠BNP＝90°，PB＝PC，
∴△PMC≌△BNP（AAS），
∴PM＝BN，MC＝PN，
∴
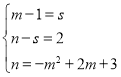，解得：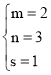
，
故点C（2，3），点P（1，1）；
故点P的坐标为（1，1）；
（3）设直线AC交y轴于点G，直线AQ交y轴于点H，
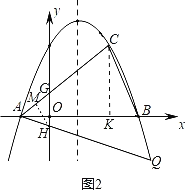
由（2）知，点C（2，3），而点A（﹣1，0），
过点C作CK⊥x轴于点K，则CK＝AK＝3，
故直线AC的倾斜角为45°，故∠AGO＝∠GAO＝45°，
∴tan∠ABC＝
＝3
∵∠QAC＝∠ABC，
∴tan∠QAC＝3；
在△AGH中，过点H作HM⊥AG于点M，设MH＝3x，
∵∠AGO＝45°，则GO＝AO＝1，
∴MG＝MH＝3x，
∵tan∠QAC＝3，则AM＝x，
AG＝AM+GM＝x+3x＝
＝，
解得：x＝
，
在△AHM中，AH＝
＝
x＝
，
在△AOH中，OH＝＝
，故点H（0，﹣），
由点A、H的坐标得，直线AH的表达式为：y＝﹣x﹣②，
联立①②并解得：x＝﹣1（舍去）或，
故点Q的坐标为：（，﹣）．
