题目内容
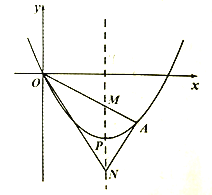
【题目】如图,某二次函数的图象是一条顶点为P(4.-4)的抛物线,它经过原点和点A,它的对称轴交线段
OA于点M.点N在对移轴上,且点M、N关于点P对称,连接AN,ON
(1)求此二次函数的解析式:
(2)若点A的坐标是(6,-3).,请直接写出MN的长
(3)若点A在抛物线的对称轴右侧运动时,则∠ANM与∠ONM有什么数量关系?并证明.
【答案】(1)y=![]() (x-4)2-4;(2)4;(3)∠ANM=∠ONM,理由见解析
(x-4)2-4;(2)4;(3)∠ANM=∠ONM,理由见解析
【解析】
(1)根据二次函数图象的顶点设出二次函数的关系式,再很据二次函数图象经过原点,求出a的值,即可得出二次函数的关系式;
(2)设直线OA的解析式为y=kx,将A点代入,求出直线OA的解析式,再把x=4代入y=-![]() x,求出M的坐标,根据点M、N关于点P对称,求出N的坐标,从而得出MN的长;
x,求出M的坐标,根据点M、N关于点P对称,求出N的坐标,从而得出MN的长;
(3)过A作AH垂直于直线l,直线l与x轴交于点D,由A在二次函数图象上,设A横坐标为m,将x=m代入二次函数解析式,表示出纵坐标,确定出A的坐标,再由O的坐标,表示出直线AO的解析式,进而表示出M,N及H的坐标,得出OD,ND,HA,及NH,在直角三角形OND中,利用锐角三角函数定义表示出tan∠ONM,在直角三角形ANH中,利用锐角三角函数定义表示出tan∠ANM,化简后得到tan∠ONM=tan∠ANM,可得出∠ONM=∠ANM,得证.
解:(1)∵二次函数图象的顶点为P(4,-4),
∴设二次函数的关系式为y=a(x-4)2-4,
又∵二次函数图象经过原点(0,0),
∴0=a(0-4)2-4,
解得a=![]() ,
,
∴二次函数的关系式为y=![]() (x-4)2-4;
(x-4)2-4;
(2)设直线OA的解析式为y=kx,将A(6,-3)代入得-3=6k,解得k=-![]() ,
,
∴直线OA的解析式为y=-![]() x,
x,
把x=4代入y=-![]() x得y=-2,
x得y=-2,
∴M的坐标是(4,-2),
又∵点M、N关于点P对称,
∴N的坐标是(4,-6),
∴MN=4,
(3)过A作AH⊥l于H,l与x轴交于点D,如图所示:
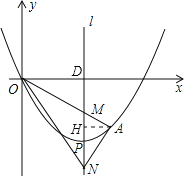
设A(m,![]() m2-2m),又O(0,0),
m2-2m),又O(0,0),
∴直线AO的解析式为y=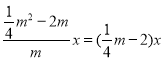
则M(4,m-8),N(4,-m),H(4,![]() m2-2m),
m2-2m),
∴OD=4,ND=m,HA=m-4,NH=ND-HD=![]() m2-m,
m2-m,
在Rt△OND中,tan∠ONM=![]() ,
,
在Rt△ANH中,tan∠ANM=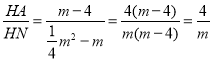
∴tan∠ONM=tan∠ANM,
则∠ANM=∠ONM.

【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .

【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了![]() 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.![]() .
.![]() 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):
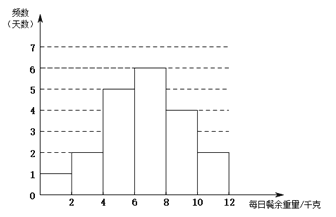
![]() .
.![]() 部门每日餐余重量在
部门每日餐余重量在![]() 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() 两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 | 平均数 | 中位数 | 众数 |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
根据以上信息,回答下列问题:
(1)写出表![]() 中的值;
中的值;
(2)在![]() 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“![]() ”或“
”或“![]() ”),理由是____________;
”),理由是____________;
(3)结合![]() 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.