题目内容
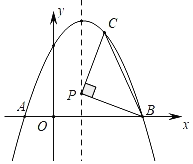
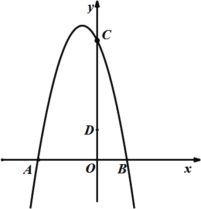
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点A、B,与
轴交于点A、B,与![]() 轴交于点C,点B的坐标为
轴交于点C,点B的坐标为![]() ,点
,点![]() 在
在![]() 轴上,连接AD.
轴上,连接AD.
(1)![]() = ;
= ;
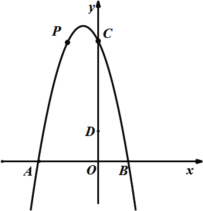
(2)若点![]() 是抛物线在第二象限上的点,过点
是抛物线在第二象限上的点,过点![]() 作PF⊥x轴,垂足为
作PF⊥x轴,垂足为![]() ,
,![]() 与
与![]() 交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点
交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标大于-4,过点
的横坐标大于-4,过点![]() 作
作![]() ,垂足为H,直线
,垂足为H,直线![]() 与
与![]() 轴交于点K,且
轴交于点K,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)2;(2)P点坐标(-2,8);(3)P点坐标为(-1,9)或(-1,9)或(![]() ,-
,-![]() ).
).
【解析】
(1)B点坐标代入二次函数得出b值;
(2)设出P点坐标,根据函数求出其余点坐标,进而求出线段长度,根据所给关系列出等式,即可求出P点坐标;
(3)延长AD交抛物线于T,过P作PF⊥x轴于F,交AD于E,根据同角的余角相等易证cos∠FAD=cos∠EPH=![]() ,进而求得PH=
,进而求得PH=![]() PE,根据已知的面积的关系式可求得PK=
PE,根据已知的面积的关系式可求得PK=![]() PH,进而求得PE,PF关系,设P点横坐标为t,可用t表示PE,PF,可列得关于t的方程,求得的t值要注意是否符合各种情况下t的取值范围.
PH,进而求得PE,PF关系,设P点横坐标为t,可用t表示PE,PF,可列得关于t的方程,求得的t值要注意是否符合各种情况下t的取值范围.
(1)∵y=-x+bx+8,B点坐标代入函数,∴b=-2;
故答案为:-2;
(2)由(1)得y=-x-2x+8,∴A点坐标(-4,0),B点坐标(2,0),
∵D点坐标为(0,2),
∴AD解析式为y=![]() x+2,
x+2,
设P(t,-t-2t+8),
∴EF=![]() +2,PE=-t-
+2,PE=-t-![]() t+6,
t+6,
若PE=7EF,则有-t-![]() t+6=7(
t+6=7(![]() +2),
+2),
解得t=-2或t=-4(舍去),
∴P点坐标为(-2,8),
故存在这样的点P,使得PE=7EF,点P的坐标为(-2,8);
(3)如图,延长AD交抛物线于T,过P作PF⊥x轴于F,交AD于E,

①若P在直线AT上方,
∵OA=4,OD=2,∠AOD=90°,
∴AD=![]() =2√5,
=2√5,
∵AH⊥PH,
∴∠FAD+∠AEF=90°,∠EPH+∠PEH=90°,∠AEF=∠PEH,
∴∠FAD=∠EPH,
∴cos∠FAD=![]() =
=![]() =
=![]() =cos∠EPH=
=cos∠EPH=![]() ,
,
∴PH=![]() PE,
PE,
∴cos∠FPK=![]() =
=![]() ,∴PK=
,∴PK=![]() PF,
PF,
∵![]() ,∴HK=
,∴HK=![]() PH,∴PK=
PH,∴PK=![]() PH,
PH,
∴![]() PF=
PF=![]() PH=
PH=![]() PE,
PE,
∴![]() =
=![]() ,
,
设P(t,-t-2t+8),
则有5(-t-2t+8)=6(-t-![]() t+6),
t+6),
得t+5t+4=0,
解得t=-1或t=-4(舍去),
∴P点坐标为(-1,9);
②若P在直线AT下方,且在x轴上方,此时S△AKA>S△PHA,与题意不符,舍去;
③若P在x轴下方,可得2PE=5PF,
得方程2(t+![]() t-6)=6(t+2t-8),
t-6)=6(t+2t-8),
得3t+5t-28=0,
解得t=![]() 或t=-4(舍去),
或t=-4(舍去),
∴P点坐标为(![]() ,-
,-![]() ),
),
综上所述,P点坐标为(-1,9)或(-1,9)或(![]() ,-
,-![]() ).
).