题目内容
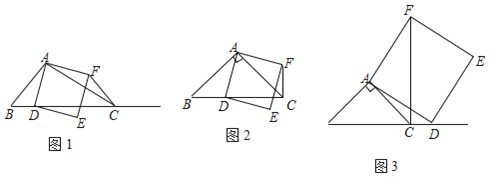
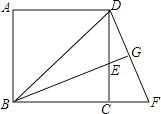
【题目】如图,有一块正方形![]() ,小王连接对角线
,小王连接对角线![]() 后,作
后,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,又将
,又将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 后到
后到![]() 的位置,并延长
的位置,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)BE的长为6.
【解析】
(1)先根据角平分线的定义得出![]() ,再根据旋转的性质可得
,再根据旋转的性质可得![]() ,从而有
,从而有![]() ,然后根据相似三角形的判定即可得证;
,然后根据相似三角形的判定即可得证;
(2)先根据(1)的结论求出DG的长,再根据正方形的性质、三角形的内角和定理得出![]() ,从而判定出
,从而判定出![]() 是等腰三角形,然后根据等腰三角形的性质得出
是等腰三角形,然后根据等腰三角形的性质得出![]() ,最后根据旋转的性质得出
,最后根据旋转的性质得出![]() ,由此即可得.
,由此即可得.
(1)![]() 平分
平分![]()
![]()
由旋转的性质得:![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]() ;
;
(2)由(1)可知:![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
由(1)可知:![]()
即![]()
![]() 是等腰三角形
是等腰三角形
![]() 是边DF上的中线(等腰三角形的三线合一)
是边DF上的中线(等腰三角形的三线合一)
![]()
由旋转的性质得:![]()
故BE的长为6.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目