ЬтФПФкШн
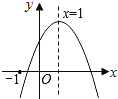
ЁОЬтФПЁПХзЮяЯпMЃКy=ax2-4ax+a-1ЃЈaЁй0ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBзѓВрЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉХзЮяЯпMЕФЖдГЦжсЪЧжБЯп______ЃЛ
ЃЈ2ЃЉЕБAB=2ЪБЃЌЧѓХзЮяЯпMЕФКЏЪ§БэДяЪНвдМАЖЅЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌжБЯпlЃКy=kx+bЃЈkЁй0ЃЉОЙ§ХзЮяЯпЕФЖЅЕуDЃЌжБЯпy=nгыХзЮяЯпMгаСНИіЙЋЙВЕуЃЌЫќУЧЕФКсзјБъЗжБ№МЧЮЊx1ЃЌx2ЃЌжБЯпy=nгыжБЯпlЕФНЛЕуЕФКсзјБъМЧЮЊx3ЃЈx3ЃМ4ЃЉЃЌШєЕБ-2ЁмnЁм-1ЪБЃЌзмгаx1-x3ЃМx3-x2ЃМ0ЃЌЧыНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГіkЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉx=2ЃЛЃЈ2ЃЉy=![]() x2+2x
x2+2x![]() ЃЌЖЅЕуDЕФзјБъЮЊЃЈ2ЃЌ
ЃЌЖЅЕуDЕФзјБъЮЊЃЈ2ЃЌ![]() ЃЉЃЛЃЈ3ЃЉkЕФШЁжЕЗЖЮЇЃК
ЃЉЃЛЃЈ3ЃЉkЕФШЁжЕЗЖЮЇЃК![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЖдГЦжсЕФЙЋЪННјааМЦЫуМДПЩЃЛ
ЃЈ2ЃЉИљОнХзЮяЯпЕФЖдГЦадвдМАЖдГЦжсЃЌЗжБ№ЧѓГіAЁЂBСНЕузјБъЃЌШЛКѓдйДњШыХзЮяЯпНтЮіЪНжаЧѓГіaжЕЃЌМДПЩНтД№ЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌЛГіКЏЪ§ЭМЯѓЃЌШЛКѓИљОнКЏЪ§ЕФЭМЯѓжБНгЧѓГіkЕФШЁжЕЗЖЮЇМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпMЃКy=ax2-4ax+a-1ЃЈaЁй0ЃЉЃЌ
ЁрХзЮяЯпЕФЖдГЦжсжБЯпЮЊЃКx=-![]() =
=![]() =2ЃЎ
=2ЃЎ
ЙЪД№АИЮЊЃКx=2ЃЛ
ЃЈ2ЃЉЁпХзЮяЯпMЃКy=ax2-4ax+a-1ЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпx=2ЃЌХзЮяЯпMгыxжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌAB=2ЃЌ
ЁрЕуAЁЂBЕФзјБъЗжБ№ЮЊЃЈ1ЃЌ0ЃЉЃЌЃЈ3ЃЌ0ЃЉЃЌ
НЋAЕФзјБъДњШыХзЮяЯпЕФКЏЪ§БэДяЪНЃЌЕУa-4a+a-1=0ЃЌ
НтЕУa=-![]() ЃЌ
ЃЌ
ЁрХзЮяЯпMЕФКЏЪ§БэДяЪНЮЊЃКy=![]() x2+2x
x2+2x![]() ЃЌ
ЃЌ
НЋХзЮяЯпMЕФКЏЪ§БэДяЪНЛЏЮЊЖЅЕуЪНЮЊЃКy=![]() x2+2x
x2+2x![]() =
=![]() ЃЈx-2ЃЉ2+
ЃЈx-2ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЖЅЕуDЕФзјБъЮЊЃЈ2ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉШчЭМЃЌгЩЃЈ2ЃЉжЊЕуDЕФзјБъЮЊЃЈ2ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпжБЯпy=nгыжБЯпlЕФНЛЕуКсзјБъМЧЮЊx3ЃЈx3ЃМ4ЃЉЃЌЧвЕБ-2ЁмnЁм-1ЪБЃЌзмгаx1-x3ЃМx3-x2ЃМ0ЃЌ
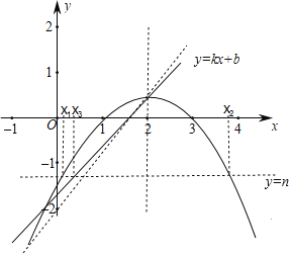
ЁржБЯпlгыyжсЕФНЛЕудкЃЈ0ЃЌ-2ЃЉЕФЯТЗНЃЌ
ЁрbЃМ-2ЃЌ
ЁпжБЯпlЃКy=kx+bЃЈkЁй0ЃЉОЙ§ХзЮяЯпЕФЖЅЕуDЃЌ
Ёр2k+b=![]() ЃЌЁрb=
ЃЌЁрb=![]() -2kЃЌ
-2kЃЌ
Ёр![]() -2kЃМ-2ЃЌНтЕУkЃО
-2kЃМ-2ЃЌНтЕУkЃО![]() ЃЎ
ЃЎ
ЙЪkЕФШЁжЕЗЖЮЇЃКkЃО![]() ЃЎ
ЃЎ