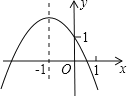Question

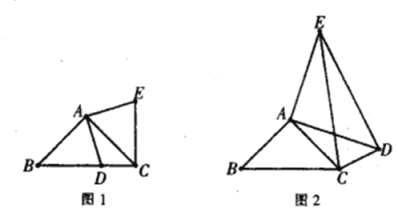
【题目】在△ABC中，点D是AB边的中点，点E为AC中点，点F在边BC上，AF交DE于点G，点H是FC的中点，连接GH．

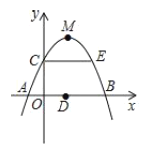
（1）如图1，求证：四边形GHCE是平行四边形；

（2）如图2，当AB＝AC，点F是BC中点时，在不添加任何辅助线的情况下，请直接写出图中所有长度等于BF的线段．

Answer 1

【答案】（1）见解析；（2）图中所有长度等于BF的线段为DG，EG，FH，CH．

【解析】

（1）根据三角形的中位线定理得到点G是AF的中点，求得HG∥CE，根据平行四边形的判定定理即可得到结论；

（2）根据三角形的中位线定理得到DG＝BF，EG＝CF，求得DG＝EG＝BF，根据平行四边形的性质得到EG＝CH，于是得到结论．

（1）∵点D是AB边的中点，点E为AC中点，

∴DE∥BC，

∴＝1，

∴点G是AF的中点，

∵点H是FC的中点，

∴HG∥CE，

∵GE∥CH，

∴四边形GHCE是平行四边形；

（2）解：由（1）知，点G是AF的中点，

∵点D是AB边的中点，点E为AC中点，

∴DG＝BF，EG＝CF，

∵点F是BC中点，

∴BF＝CF，

∴DG＝EG＝BF，

∵四边形GHCE是平行四边形；

∴EG＝CH，

∵点H是FC的中点，

∴CH＝FH＝EG，

∴DG＝EG＝FH＝CH＝BF，

即图中所有长度等于BF的线段为DG，EG，FH，CH．