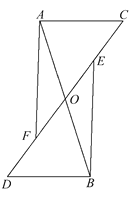
题目内容
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
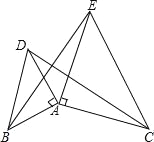
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
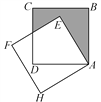
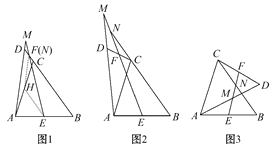
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
【答案】(1)∠AMF=∠ENB；(2)∠AMF=∠ENB，∠AMF+∠ENB=180°，证明见解析.
【解析】
(1) 取AC的中点H，连接HE、HF，当点D旋转到图2中的位置时，由F为DC的中点，E为AB的中点，根据三角形中位线的性质得到FH∥AD，且FH=
AD；HE∥BC，且HE=BC，得到∠HFE=∠AMF，∠HEF=∠ENB，HE=HF，则∠HEF=∠HFE，所以∠AMF=∠BNE；当点D旋转到图3中的位置时，同理可证得∠AMF=∠BNE．
(2) 与（1）相同，都需要作出两条辅助线，两次运用中位线定理解答．
(1)图1:∠AMF=∠ENB.
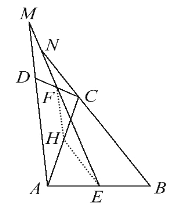
(2)图2:∠AMF=∠ENB;
图3:∠AMF+∠ENB=180°.
当点D旋转到图2中的位置时，
证明:如图,取AC的中点H,
连接HE,HF.
∵F是DC的中点,H是AC的中点,
∴HF∥AD,HF=AD,
∴∠AMF=∠HFE,
同理,HE∥CB,HE=CB,∴∠ENB=∠HEF.
∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,
∴∠ENB=∠AMF.
当点D旋转到图3中的位置时，
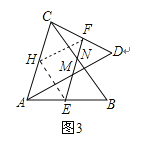
用同样的方法可证明∠HFE=∠AME，∠HEF=∠BNE，
而∠HFE=∠HEF，
∴∠AME=∠BNE，
而∠AMF+∠AME=180°，
∴∠AMF+∠BNE=180°．
故答案为：∠AMF=∠BNE或∠AMF+∠BNE=180°．
