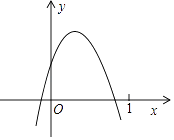ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy= ![]() x2Љ
x2Љ ![]() x+3
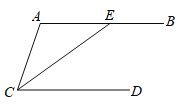
x+3 ![]() гыxжсНЛгкЕуAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЙ§ЕуCзїCDЁЮxжсЃЌЧвНЛХзЮяЯпгкЕуDЃЌСЌНгADЃЌНЛyжсгкЕуEЃЌСЌНгACЃЎ
гыxжсНЛгкЕуAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЙ§ЕуCзїCDЁЮxжсЃЌЧвНЛХзЮяЯпгкЕуDЃЌСЌНгADЃЌНЛyжсгкЕуEЃЌСЌНгACЃЎ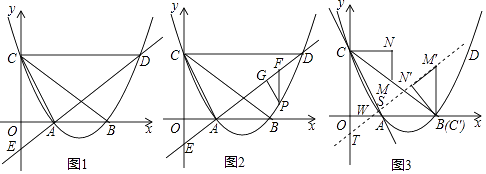
ЃЈ1ЃЉЧѓSЁїABDЕФжЕЃЛ
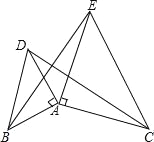
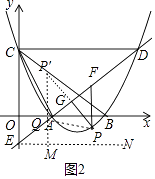
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуPЪЧжБЯпADЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPFЁЮyжсНЛжБЯпADгкЕуFЃЌзїPGЁЮACНЛжБЯпADгкЕуGЃЌЕБЁїPGFЕФжмГЄзюДѓЪБЃЌдкЯпЖЮDEЩЯШЁвЛЕуQЃЌЕБPQ+ ![]() QEЕФжЕзюаЁЪБЃЌЧѓДЫЪБPQ+
QEЕФжЕзюаЁЪБЃЌЧѓДЫЪБPQ+ ![]() QEЕФжЕЃЛ
QEЕФжЕЃЛ
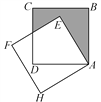
ЃЈ3ЃЉШчЭМ3ЃЌMЪЧBCЕФжаЕуЃЌвдCMЮЊаББпзїжБНЧЁїCMNЃЌЪЙCNЁЮxжсЃЌMNЁЮyжсЃЌНЋЁїCMNбиЩфЯпCBЦНвЦЃЌМЧЦНвЦКѓЕФШ§НЧаЮЮЊЁїCЁфMЁфNЁфЃЌЕБЕуNЁфТфдкxжсЩЯМДЭЃжЙдЫЖЏЃЌНЋДЫЪБЕФЁїCЁфMЁфNЁфШЦЕуCЁфФцЪБеыа§зЊЃЈа§зЊЖШЪ§ВЛГЌЙ§180ЁуЃЉЃЌа§зЊЙ§ГЬжажБЯпMЁфNЁфгыжБЯпCAНЛгкЕуSЃЌгыyжсНЛгкЕуTЃЌгыxжсНЛгкЕуWЃЌЧыЮЪЁїCSTЪЧЗёФмЮЊЕШбќШ§НЧаЮЃПШєФмЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФWNЁфЕФГЄЖШЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКСюy=0ЃЌдђ2 ![]() x2Љ33x+36
x2Љ33x+36 ![]() =0ЃЌ
=0ЃЌ
НтЕУx= ![]() Лђ4
Лђ4 ![]() ЃЎ
ЃЎ
ЁрAЃЈ ![]() ЃЌ0ЃЉЃЌBЃЈ4
ЃЌ0ЃЉЃЌBЃЈ4 ![]() ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3
ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3 ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпCDЁЮABЃЌ
ЁрSЁїDAB=SЁїABC= ![]() ABOC=
ABOC= ![]() ЁС
ЁС ![]() ЁС
ЁС ![]() =
= ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉНтЃКШчЭМ2жаЃЌЩшPЃЈmЃЌ ![]() m2Љ
m2Љ ![]() m+3
m+3 ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпAЃЈ ![]() ЃЌ0ЃЉЃЌDЃЈ
ЃЌ0ЃЉЃЌDЃЈ ![]() ЃЌ3
ЃЌ3 ![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпADЕФНтЮіЪНЮЊy= ![]() xЉ
xЉ ![]() ЃЌ
ЃЌ
ЁпPFЁЮyжсЃЌ
ЁрFЃЈmЃЌ ![]() mЉ
mЉ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпPGЁЭDEЃЌ
ЁрЁїPGFЕФаЮзДЪЧЯрЫЦЕФЃЌ
ЁрPFЕФжЕзюДѓЪБЃЌЁїPFGЕФжмГЄзюДѓЃЌ
ЁпPF= ![]() mЉ
mЉ ![]() ЉЃЈ
ЉЃЈ ![]() m2Љ
m2Љ ![]() m+3
m+3 ![]() ЃЉ=Љ
ЃЉ=Љ ![]() m2+
m2+ ![]() mЉ
mЉ ![]() ЃЌ
ЃЌ
ЁрЕБm=Љ ![]() =
= ![]() ЪБЃЌPFЕФжЕзюДѓЃЌДЫЪБPЃЈ
ЪБЃЌPFЕФжЕзюДѓЃЌДЫЪБPЃЈ ![]() ЃЌЉ
ЃЌЉ ![]() ЃЉЃЌ
ЃЉЃЌ
зїPЙигкжБЯпDEЕФЖдГЦЕуPЁфЃЌСЌНгPЁфQЃЌPQЃЌзїENЁЮxжсЃЌQMЁЭENгкMЃЌ
ЁпЁїQEMЁзЁїEAOЃЌ
Ёр ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрQM= ![]() QEЃЌ
QEЃЌ
ЁрPQ+ ![]() EQ=PQ+QM=PЁфQ+QMЃЌ
EQ=PQ+QM=PЁфQ+QMЃЌ
ЁрЕБPЁфЁЂQЁЂMЙВЯпЪБЃЌPQ+ ![]() EQЕФжЕзюаЁЃЌ
EQЕФжЕзюаЁЃЌ
взжЊжБЯпPPЁфЕФНтЮіЪНЮЊy=Љ ![]() x+
x+ ![]() ЃЌ
ЃЌ
гЩ 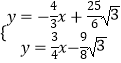 ЃЌПЩЕУGЃЈ
ЃЌПЩЕУGЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпPG=GPЁфЃЌ
ЁрPЁфЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрPЁфM= ![]() +
+ ![]() =
= ![]() ЃЌ
ЃЌ
ЁрPQ+ ![]() EQЕФзюаЁжЕЮЊ
EQЕФзюаЁжЕЮЊ ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉНтЃКЂйШчЭМ3жаЃЌЕБCS=CTЪБЃЌзїCKЦНЗжЁЯOCAЃЌзїKGЁЭACгкGЃЎ
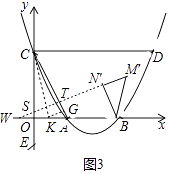
взжЊKO=KGЃЌ
Ёп ![]() =
= ![]() =
=  =
= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрOK= ![]()
![]() =3
=3 ![]() Љ6
Љ6 ![]() ЃЌ
ЃЌ
взжЄЁЯBWNЁф=ЁЯOCKЃЌ
ЁрtanЁЯBWNЁф=tanЁЯOCK= ![]() =
= ![]() ЃЌ
ЃЌ
ЁпBNЁф=2 ![]() ЃЌ
ЃЌ
ЁрWNЁф=2 ![]() +4
+4 ![]() ЃЎ
ЃЎ
ЂкШчЭМ4жаЃЌЕБTC=TSЪБЃЌ
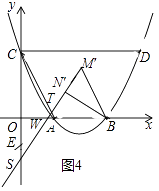
взжЄЁЯBWNЁф=ЁЯOACЃЌ
ЁрtanЁЯBWNЁф=tanЁЯOAC= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрWNЁф= ![]() ЃЌ
ЃЌ
ЂлШчЭМ5жаЃЌЕБTS=TCЪБЃЌбгГЄNЁфBНЛжБЯпACгкQЃЌзїBGЁЭAQгкGЃЌQRЁЭABгкRЃЎ

ЁпTS=TCЃЌ
ЁрЁЯTSC=ЁЯTCS=ЁЯACOЃЌ
ЁпЁЯTSC+ЁЯSQNЁф=90ЁуЃЌЁЯACO+ЁЯOAC=90ЁуЃЌ
ЁрЁЯBQA=ЁЯOAC=ЁЯBAQЃЌ
ЁрBA=BQЃЌ
ЁрAG=GQЃЌЩшAQ=aЃЌдђвзжЊBG=aЃЌBQ=AB= ![]() aЃЌ
aЃЌ
Ёп ![]() AQBG=
AQBG= ![]() ABQRЃЌ
ABQRЃЌ
ЁрQR= aЃЌBR=
![]() aЃЌ
aЃЌ
ЁрtanЁЯWBNЁф=tanЁЯQBR= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрWNЁф= ![]() ЃЎ
ЃЎ
ЂмШчЭМ6жаЃЌЕБCS=CTЪБЃЌ
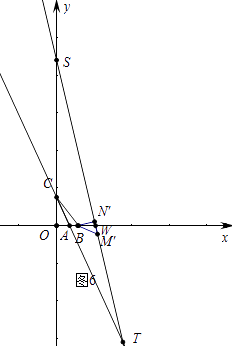
гЩЂйПЩжЊЃЌдкRtЁїBNЁфWжаЃЌtanЁЯNЁфBW= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрNЁфW=2 ![]() Љ4
Љ4 ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФWNЁфЕФГЄЮЊ2 ![]() +4
+4 ![]() Лђ
Лђ ![]() Лђ
Лђ ![]() Лђ2
Лђ2 ![]() Љ4
Љ4 ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉСюy=0ЃЌДњШыХзЮяЯпЕФНтЮіЪНЃЌЧѓГіA,B,CЕФзјБъЃЌгЩCDЁЮABЃЌЭЦГіSЁїDAB=SЁїABCЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЪзЯШЫЕУїPFЕФжЕзюДѓЪБЃЌЁїPFGЕФжмГЄзюДѓЃЌШЛКѓЫЕУїЕБЕБm=-![]() =
= ![]()
![]() ЪБ,PFЕФжЕзюДѓЃЌДЫЪБPЃЈ
ЪБ,PFЕФжЕзюДѓЃЌДЫЪБPЃЈ![]()
![]() ЃЌ
ЃЌ![]()
![]() ЃЉЃЌзїPЙигкжБЯпDEЕФЖдГЦЕуPЁфЃЌСЌНгPЁфQЃЌPQЃЌзїENЁЮxжсЃЌQMЁЭENгкMЃЌгЩЁїQEMЁзЁїEAOЖдгІБпГЩБШР§ЭЦГіQM=
ЃЉЃЌзїPЙигкжБЯпDEЕФЖдГЦЕуPЁфЃЌСЌНгPЁфQЃЌPQЃЌзїENЁЮxжсЃЌQMЁЭENгкMЃЌгЩЁїQEMЁзЁїEAOЖдгІБпГЩБШР§ЭЦГіQM= ![]() QEЃЌЭЦГіPQ+
QEЃЌЭЦГіPQ+ ![]() EQ=PQ+QM=PЁфQ+QMЃЌЭЦГіP,Q,MШ§ЕуЙВЯпЪБЃЌPQ+
EQ=PQ+QM=PЁфQ+QMЃЌЭЦГіP,Q,MШ§ЕуЙВЯпЪБЃЌPQ+ ![]() EQЕФжЕзюаЁЃЌвзжЊжБЯпPPЁфЕФНтЮіЪНЃЌСЊЯЕжБЯпADЕФНтЮіЪНгыжБЯпPPЁфЕФНтЮіЪНЧѓГіGЕуЕФзјБъЃЌНјЖјевЕНPЁфЕФзјБъЃЌЕУЕНPЁфMЕФГЄЖШМДПЩЃЛ
EQЕФжЕзюаЁЃЌвзжЊжБЯпPPЁфЕФНтЮіЪНЃЌСЊЯЕжБЯпADЕФНтЮіЪНгыжБЯпPPЁфЕФНтЮіЪНЧѓГіGЕуЕФзјБъЃЌНјЖјевЕНPЁфЕФзјБъЃЌЕУЕНPЁфMЕФГЄЖШМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃКЂйШчЭМ3жаЃЌЕБCS=CTЪБЃЌзїCKЦНЗжЁЯOCAЃЌзїKGЁЭACгкGЃЌгЩtanЁЯBWNЁф=tanЁЯOCKЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЌЂкШчЭМ4жаЃЌЕБTC=TSЪБЃЌгЩtanЁЯBWNЁф=tanЁЯOACЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЁЃ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪКЭа§зЊЕФаджЪЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеЯрЫЦШ§НЧаЮЕФвЛЧаЖдгІЯпЖЮ(ЖдгІИпЁЂЖдгІжаЯпЁЂЖдгІНЧЦНЗжЯпЁЂЭтНгдВАыОЖЁЂФкЧадВАыОЖЕШЃЉЕФБШЕШгкЯрЫЦБШЃЛЯрЫЦШ§НЧаЮжмГЄЕФБШЕШгкЯрЫЦБШЃЛЯрЫЦШ§НЧаЮУцЛ§ЕФБШЕШгкЯрЫЦБШЕФЦНЗНЃЛЂйа§зЊКѓЖдгІЕФЯпЖЮГЄЖЬВЛБфЃЌа§зЊНЧЖШДѓаЁВЛБфЃЛЂка§зЊКѓЖдгІЕФЕуЕНа§зЊЕНа§зЊжааФЕФОрРыВЛБфЃЛЂла§зЊКѓЮяЬхЛђЭМаЮВЛБфЃЌжЛЪЧЮЛжУБфСЫВХФме§ШЗНтД№ДЫЬтЃЎ