题目内容
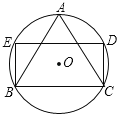
【题目】如图，等边三角形ABC内接于半径为1的⊙O，以BC为一边作⊙O的内接矩形BCDE，求矩形BCDE的面积 .
【答案】
【解析】试题分析：连接BD，由等边三角形的性质和圆周角定理得出∠BDC=∠BAC=60°，由矩形的性质和圆周角定理证出BD是⊙O的直径，得出BD=2，CD=
BD=1，由勾股定理得出BC的长，即可求出矩形BCDE的面积．
试题解析：解：连接BD，如图所示：
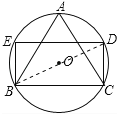
∵△ABC是等边三角形，∴∠BAC=60°，∴∠BDC=∠BAC=60°．
∵四边形BCDE是矩形，∴∠BCD=90°，∴BD是⊙O的直径，∠CBD=90°-60°=30°，
∴BD=2，CD=
BD=1，∴BC=
=
，∴矩形BCDE的面积=BCCD=
=
．
练习册系列答案
相关题目
【题目】某学习小组在研究函数y=
x3﹣2x的图象与性质时，已列表、描点并画出了图象的一部分．
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
（1）请补全函数图象；
（2）方程
x3﹣2x=﹣2实数根的个数为 ；
（3）观察图象，写出该函数的两条性质．
【题目】二次函数y= ax+bx＋c,自变量x 与函数y 的对应值如表:
x | ... | －5 | －4 | －3 | －2 | －1 | 0 | ... |
y | ... | 4 | 0 | －2 | －2 | 0 | 4 | ... |
下列说法正确的是（ ）
A. 抛物线的开口向下 B. 当x>-3时，y随x的增大而增大
C. 二次函数的最小值是－2 D. 抛物线的对称轴是x＝－5/2
