题目内容
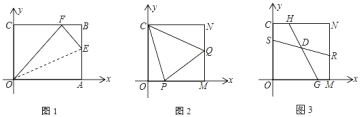
【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF
,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值;
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.

【答案】(1)4,3;(2)当点F在线段AB上时,![]() ;当点F在线段AD上时,
;当点F在线段AD上时,![]() ;
;
(3)存在,![]() 或
或![]() 或
或![]() 或
或![]() ..
..
【解析】
(1)利用矩形性质、勾股定理及三角形面积公式求解;
(2)依题意画出图形,如答图2所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;
(3)在旋转过程中,等腰△DPQ有4种情形,如答图3所示,对于各种情形分别进行计算.
解:(1)在Rt△ABD中,AB=5,AD=![]() ,
,
由勾股定理得:BD=![]() =
=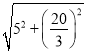 =
=![]() .
.
∵![]() =
=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=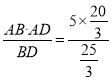 =4.
=4.
在Rt△ABE中,AB=5,AE=4,
由勾股定理得:BE=3;
(2)设平移中的三角形为△A′B′F′,如答图2所示:
由对称点性质可知,∠1=∠2.
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.
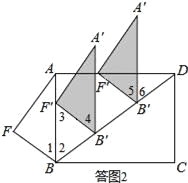
①当点F′落在AB上时,
∵AB∥A′B′,
∴∠3=∠4,
∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②当点F′落在AD上时,
∵AB∥A′B′,
∴∠6=∠2,
∵∠1=∠2,∠5=∠1,
∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D为等腰三角形,
∴B′D=B′F′=3,
∴BB′=BD﹣B′D=![]() ﹣3=
﹣3=![]() ,即m=
,即m=![]() ;
;
(3)存在.理由如下:
在旋转过程中,等腰△DPQ依次有以下4种情形:
①如答图3﹣1所示,点Q落在BD延长线上,且PD=DQ,易知∠2=2∠Q,

∵∠1=∠3+∠Q,∠1=∠2,
∴∠3=∠Q,
∴A′Q=A′B=5,
∴F′Q=F′A′+A′Q=4+5=9.
在Rt△BF′Q中,由勾股定理得:BQ=![]() =
=![]() .
.
∴DQ=BQ﹣BD=![]() ;
;
②如答图3﹣2所示,点Q落在BD上,且PQ=DQ,易知∠2=∠P,
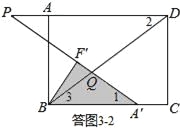
∵∠1=∠2,
∴∠1=∠P,
∴BA′∥PD,则此时点A′落在BC边上.
∵∠3=∠2,
∴∠3=∠1,
∴BQ=A′Q,
∴F′Q=F′A′﹣A′Q=4﹣BQ.
在Rt△BQF′中,由勾股定理得:![]() ,
,
即![]() ,
,
解得:BQ=![]() ,
,
∴DQ=BD﹣BQ=![]() =
=![]() ;
;
③如答图3﹣3所示,点Q落在BD上,且PD=DQ,易知∠3=∠4.
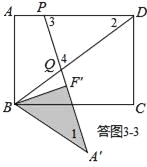
∵∠2+∠3+∠4=180°,∠3=∠4,
∴∠4=90°﹣![]() ∠2.
∠2.
∵∠1=∠2,
∴∠4=90°﹣![]() ∠1.
∠1.
∴∠A′QB=∠4=90°﹣![]() ∠1,
∠1,
∴∠A′BQ=180°﹣∠A′QB﹣∠1=90°﹣![]() ∠1,
∠1,
∴∠A′QB=∠A′BQ,
∴A′Q=A′B=5,
∴F′Q=A′Q﹣A′F′=5﹣4=1.
在Rt△BF′Q中,由勾股定理得:BQ=![]() =
=![]() ,
,
∴DQ=BD﹣BQ=![]() ;
;
④如答图3﹣4所示,点Q落在BD上,且PQ=PD,易知∠2=∠3.
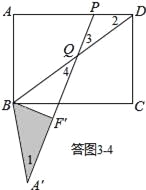
∵∠1=∠2,∠3=∠4,∠2=∠3,
∴∠1=∠4,
∴BQ=BA′=5,
∴DQ=BD﹣BQ=![]() ﹣5=
﹣5=![]() .
.
综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形;
DQ的长度分别为![]() 或
或![]() 或
或![]() 或
或![]() .
.

【题目】某校七(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:
次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | a | 4 | 12 | 16 | 8 | 3 |
结合图表完成下列问题:
(1)a= ,全班人数是______;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀学生人数占全班总人数的百分之几?

【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价-进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.