Question

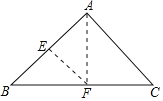
【题目】如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=cm， 则BC的长是_______________ ．

Answer 1

【答案】cm

【解析】

由折叠的性质可知∠B=∠EAF=45°，所以可求出∠AFB=90°，再直角三角形的性质可知EF=AB，所以AB、AC的长可求，再利用勾股定理即可求出BC的长．

解：∵AB=AC，∠BAC=90°，

∴∠B=∠C=45°，

∵沿过点E的直线折叠，使点B与点A重合，

∴∠B=∠EAF=45°，

∴∠AFB=90°，

∵点E为AB中点，

∴EF=AB，EF= cm，

∴AB=AC=3 cm，

∵∠BAC=90°，

∴BC=cm．

故答案为：cm．