题目内容
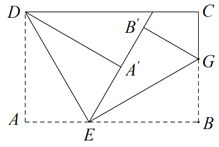
【题目】如图,将长方形纸片的一角作折叠，使顶点 A 落在 A处, DE 为折痕，将 BEA对折，使得 B落在直线 EA上，得折痕 EG .
(1)求 DEG 的度数；
(2) 若 EA恰好平分 DEB ，求 DEA的度数 .
【答案】（1）90°；（2）60°．
【解析】
（1）由折叠的性质可得∠A'ED=∠AED，∠BEG=∠B'EG，又因为∠AEB=180°从而可求得∠DEG；
（2）由角平分线的性质及∠DEG的度数即可得出结论．
（1）由折叠的性质可得∠A'ED=∠AED，∠BEG=∠B'EG，∴∠DEG=∠DEB'+∠B'EG=180°÷2=90°；
（2）∵EA恰好平分 DEB，∴∠DEA′=∠BEA′．
∵∠BEG=∠B'EG，∴∠DEA′=2∠GEB′．
∵∠DEG=90°，∴∠GEB′=30°，∴∠DEA′=60°．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
