题目内容
【题目】如图,平行四边形![]() .
.
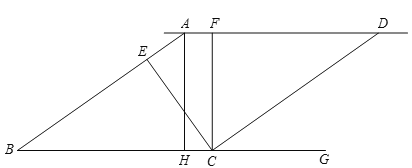
(1)如图,点![]() 在
在![]() 延长线上,
延长线上,![]() ,求证:点
,求证:点![]() 为
为![]() 中点.
中点.

(2)如图,点![]() 在
在![]() 中点,
中点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() .
.
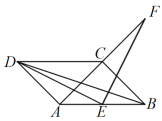
(3)在(2)的条件下,若![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,试判断四边形
,试判断四边形![]() 是否为平行四边形?并证明你的结论(先补全图形再解答).
是否为平行四边形?并证明你的结论(先补全图形再解答).

【答案】(1)见详解;(2)见详解;(3)四边形ACPE是平行四边形,补图与证明见详解.
【解析】
(1)先由平行四边形ABCD可得AD∥BC,AD=BC,再证四边形BDEC为平行四边形可得BC=DE,再等量代换即可得证;
(2)连接CE,根据三线合一可证得∠AEC=90°,结合∠DEF=90°,可得∠AED=∠CEF,根据∠ACB=90°,E为AB中点可得CE=AE,再结合∠DAE=∠ECF=135°即可证得△DAE≌△ECF进而得证;
(3)四边形ACPE是平行四边形,理由如下:先证得∠CEB=∠EBP=∠ECP=90°可得矩形BECP,进而得CP=BE等量代换得AE=CP,再结合AE∥CP即可得证.
证明:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵AD∥BC,CE∥BD,
∴四边形BDEC为平行四边形,
∴BC=DE,
又∵AD=BC,
∴AD= DE,
∴点D为AE中点.
(2)如图,连接CE,
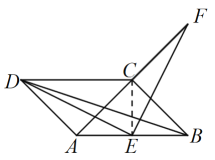
∵AD⊥AC,AD∥BC,
∴∠ACB=∠DAC=90°,
∵AD=BC,AD=AC,
∴BC=AC,
∵BC=AC,点E为AB中点,
∴CE⊥AB,
∴∠AEC=∠BEC=90°,
∴∠AED+∠DEC=90°,
∵ED⊥EF,
∴∠CEF+∠DEC=∠DEF=90°,
∴∠CEF=∠AED,
∵∠ACB=90°,BC=AC,
∴∠CAB=∠CBA=45°,
∴∠DAE=∠DAC+∠CAB=135°,
∵∠ACB=90°,点E为AB中点,
∴CE=AE=![]() AB,
AB,
∴∠ACE=∠CAB=45°,
∴∠FCE=180°-∠ACE=135°,
∴∠FCE=∠DAE,
在△DAE和△FCE中,
 ,
,
∴△DAE≌△FCE(ASA),
∴DE=EF.
(3)如图,

四边形ACPE是平行四边形,理由如下:
∵△DAE≌△FCE,
∴AD=CF,
∵AD=BC,
∴BC=CF,
又∵∠FCB=180°-∠ACB=90°,
∴∠CBF=∠CFB=45°,
∵∠CBA=45°,
∴∠EBF=∠CBF+∠CBA=90°,
∵AB∥CD,∠BEC=90°,
∴∠ECP=180°-∠BEC=90°,
∴∠ECP=∠BEC=∠EBF=90°,
∴四边形BECP为矩形,
∴BE=CP,
又∵AE=BE,
∴AE=CP,
∵AE=CP,AE∥CP,
∴四边形ACPE是平行四边形.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案