题目内容
如图1,△ABC为等边三角形,面积为S.D1,E1,F1分别是△ABC三边上的点,且AD1=BE1=CF1=
AB,连接D1E1,E1F1,F1D1,可得△D1E1F1.
(1)用S表示△AD1F1的面积S1=
,△D1E1F1的面积S1′=
;
(2)当D2,E2,F2分别是等边△ABC三边上的点,且AD2=BE2=CF2=
AB时,如图②,求△AD2F2的面积S2和△D2E2F2的面积S2′;
(3)按照上述思路探索下去,当Dn,En,Fn分别是等边△ABC三边上的点,且ADn=BEn=CFn=
AB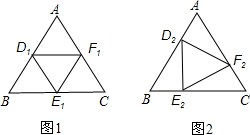 时(n为正整数),求△ADnFn的面积Sn,△DnEnFn的面积Sn′.
时(n为正整数),求△ADnFn的面积Sn,△DnEnFn的面积Sn′.
| 1 |
| 2 |
(1)用S表示△AD1F1的面积S1=
| 1 |
| 4 |
| 1 |
| 4 |
(2)当D2,E2,F2分别是等边△ABC三边上的点,且AD2=BE2=CF2=
| 1 |
| 3 |
(3)按照上述思路探索下去,当Dn,En,Fn分别是等边△ABC三边上的点,且ADn=BEn=CFn=
| 1 |
| n+1 |
 时(n为正整数),求△ADnFn的面积Sn,△DnEnFn的面积Sn′.
时(n为正整数),求△ADnFn的面积Sn,△DnEnFn的面积Sn′.(1)设等边△ABC的边长是a,
∵AD1=AF1,∠A=60°,
∴△AD1F1是等边三角形,
同理其余三个三角形都是等边三角形,
∴△AD1F1≌△BE1D1≌△CF1E1≌△D1E1F1,
∴S1=
S,S1'=
S.
(2)设△ABC的边长为a,则△AD2F2的面积S2=
AD2•AF2sin∠A=
•
a•
a•sin60°=
,
又因为△ABC的面积S=
a2,所以S2=
S,
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
又∵AD2=BE2=CF2,AF2=BD2=CE2,
由“SAS”得出△AD2F2≌△BE2D2≌△CF2E2,
∴S2′=S-3S2=S-3×
S=
S.
(3)设△ABC的边长是a,
则Sn=
•
a•
a•sin60°=
S,
同理证明△ADnFn≌△BEnDn≌△CFnEn,
∴Sn′=S-3×
S=
S.
∵AD1=AF1,∠A=60°,
∴△AD1F1是等边三角形,
同理其余三个三角形都是等边三角形,
∴△AD1F1≌△BE1D1≌△CF1E1≌△D1E1F1,
∴S1=
| 1 |
| 4 |
| 1 |
| 4 |
(2)设△ABC的边长为a,则△AD2F2的面积S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 9×2 |
又因为△ABC的面积S=
| ||
| 4 |
| 2 |
| 9 |
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
又∵AD2=BE2=CF2,AF2=BD2=CE2,
由“SAS”得出△AD2F2≌△BE2D2≌△CF2E2,
∴S2′=S-3S2=S-3×
| 2 |
| 9 |
| 1 |
| 3 |
(3)设△ABC的边长是a,
则Sn=
| 1 |
| 2 |
| 1 |
| n+1 |
| n |
| n+1 |
| n |
| (n+1)2 |
同理证明△ADnFn≌△BEnDn≌△CFnEn,
∴Sn′=S-3×
| n |
| (n+1)2 |
| n2-n+1 |
| (n+1)2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






