题目内容
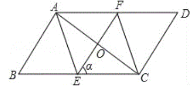
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C. D. E三点不在同一直线上时,以ED、EC我邻边作ECFD,设点D运动的时间为t(秒).
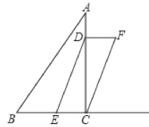
(1)用含t的代数式表示CE的长度。
(2)当F点落在△ABC的内部时,求t的取值范围。
(3)设ECFD的面积为S(平方单位),求S与t之间的函数关系式。
(4)当点F到Rt△ABC的一条直角边的距离是到另一条直角边距离的2倍时,直接写出ECFD的面积.
【答案】(1)当0t<![]() 时,CE= 32t;当
时,CE= 32t;当![]() t4时,CE= 2t3;(2)
t4时,CE= 2t3;(2)![]() <t<
<t<![]() ;(3)S=
;(3)S= ;(4)
;(4)![]() 或2或
或2或![]() .
.
【解析】
(1)分两种情形分别求出CE的长即可;
(2)求出点F落在AB或AC上的时间即可解决问题.
(3)分两种情形求解即可;
(4)分四种情形列出方程求解即可解决问题;
(1)由题意,BE=2t,
当点E与点C重合时,2t=3,
∴t=![]() ,
,
当点D与点C重合时,t=4.
∴当0t<![]() 时,CE=BCBE=32t.
时,CE=BCBE=32t.
当![]() t4时,CE=BEBC=2t3.
t4时,CE=BEBC=2t3.
(2)当F落在AB上时,tanA=![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
当点F落在AC边上时,点E与点C重合,
∴t=![]() ,
,
∴当点F落在△ABC的内部时, ![]() <t<
<t<![]() .
.
(3)当0t<![]() 时,S=ECDC=(32t)(4t)=2t
时,S=ECDC=(32t)(4t)=2t![]() 11t+12.
11t+12.
当![]() <t<4时,S=ECDC=(2t3)(4t)=2t
<t<4时,S=ECDC=(2t3)(4t)=2t![]() +11t12,
+11t12,
综上所述,S= .
.
(4)由题意DC=2DF或DF=2DC,
则有4t=2(32t),解得t=![]() ,此时S=
,此时S=![]()
或32t=2(4t),无解,不存在,
或4t=2(2t3),解得t=2,此时S=2,
或2t3=2(4t),解得t=114,此时S=![]() ,
,
∴ECFD的面积为![]() 或2或
或2或![]() .
.