题目内容
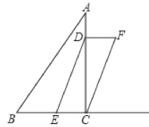
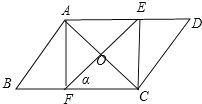
【题目】如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α。
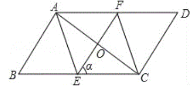
(1)当α的度数是_________时,四边形AFCE为菱形;
(2)当α的度数是_________时,四边形AFCE为矩形;
(3)四边形AFCE能否为正方形?为什么?
【答案】(1)60;(2)30;(3)不能
【解析】
(1)当α的度数是60°时,四边形AFCE为菱形,首先证明四边形AFCE、四边形AFEB是平行四边形,再证明△ABE是等边三角形即可解决问题.
(2)当α的度数是30°时,四边形AFCE为矩形,取BC中点M,连接AM,首先证明△ABM是等边三角形,推出∠OCE=30°即可解决问题.
(3)不可能,只要证明AE≠AF即可解决问题.
(1)当α的度数是60°时,四边形AFCE为菱形,理由如下:
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAO=∠ECO.
在△AOF和△COE中,∵ ,∴△AOF≌△COE(ASA),∴OE=OF.
,∴△AOF≌△COE(ASA),∴OE=OF.
∵OA=OC,∴四边形AFCE是平行四边形,∴AF=CE,AF∥BC,∴AF∥BE.
∵∠α=∠ABC=60°,∴AB∥EF,∴四边形AFEB是平行四边形,∴AF=BE=CE.
∵BC=8,AB=4,∴AB=BE=4.
∵∠B=60°,∴△ABE是等边三角形,∴AE=BE=CE.
∵四边形AFCE是平行四边形,∴四边形AFCE是菱形.
故答案为:60°;

(2)当α的度数是30°时,四边形AFCE为矩形,理由如下:
同(1)得:四边形AFCE是平行四边形,取BC中点M,连接AM.
∵AB=BM=4,∠B=60°,∴△ABM是等边三角形,∴∠AMB=60°,AM=BM=AB=CM,∴∠ACM=∠MAC=30°.
∵∠α=30°,∴∠OEC=∠OCE,∴OE=OC.
∵OE=OF,OA=OC,∴AC=EF,∴四边形AECF是矩形.
故答案为:30°.
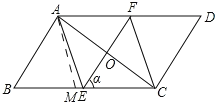
(3)四边形AECF不可能是正方形.
理由如下:如图四边形AFCE是矩形.
∵AB=4,BC=8,∠B=60°,∴在Rt△ABF中,AF=ABsin∠B=2![]() ,BF=ABcos60°=2,∴CF=BC﹣BF=8﹣2=6.
,BF=ABcos60°=2,∴CF=BC﹣BF=8﹣2=6.
∵AF≠FC,∴四边形AFCE不是正方形.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某班数学兴趣小组对函数y=|x2﹣2x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围取足全体实数,x与y的几组对应值列表如下:其中m= .
x | …… | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | …… |
y | …… | 3 | m | 0 | 0.75 | 1 | 0.75 | 0 | 1.25 | 3 | …… |
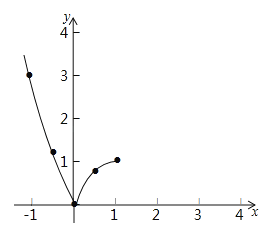
(2)根括上表数据,在如图所示的平面直角坐标系中描点,现在画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出函数的一条性质 ;
(4)进一步探究函数图象解决问题:
①方程|x2﹣2x|=![]() 有 个实数根;
有 个实数根;
②在(2)问的平面直角坐标系中画出直线y=﹣x+1,根据图象写出方程|x2﹣2x|=﹣x+1的一个正数根约为 .(精确到0.1)